Tight Regret Bounds for Noisy Optimization of a Brownian Motion
Paper and Code
Jan 25, 2020
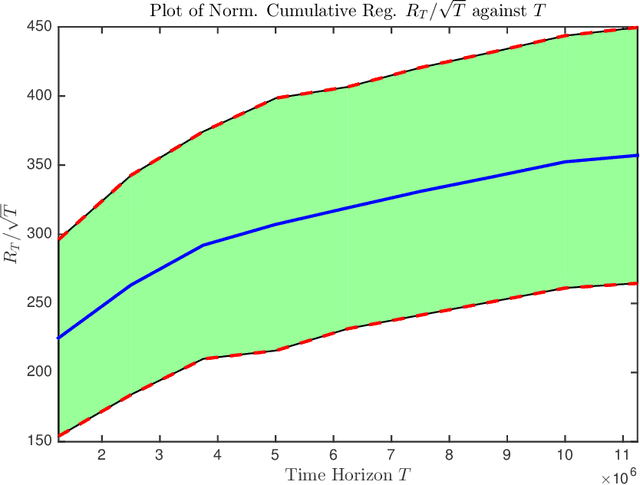
We consider the problem of Bayesian optimization of a one-dimensional Brownian motion in which the $T$ adaptively chosen observations are corrupted by Gaussian noise. We show that as the smallest possible expected simple regret and the smallest possible expected cumulative regret scale as $\Omega(1 / \sqrt{T \log (T)}) \cap \mathcal{O}(\log T / \sqrt{T})$ and $\Omega(\sqrt{T / \log (T)}) \cap \mathcal{O}(\sqrt{T} \cdot \log T)$ respectively. Thus, our upper and lower bounds are tight up to a factor of $\mathcal{O}( (\log T)^{1.5} )$. The upper bound uses an algorithm based on confidence bounds and the Markov property of Brownian motion, and the lower bound is based on a reduction to binary hypothesis testing.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge