Thresholding Bandit for Dose-ranging: The Impact of Monotonicity
Paper and Code
Jul 24, 2018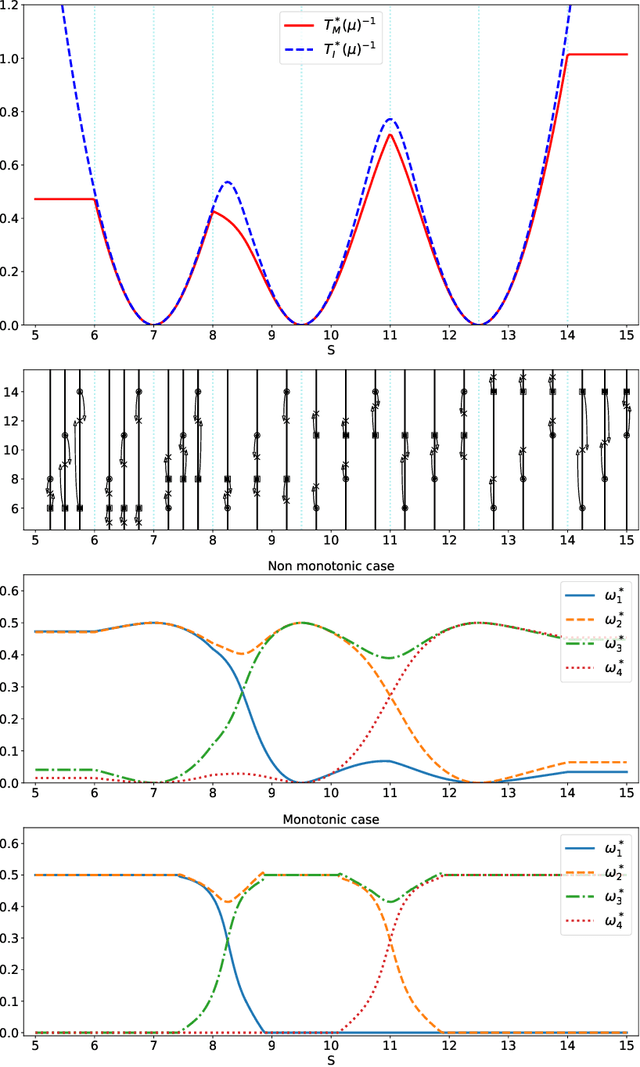


We analyze the sample complexity of the thresholding bandit problem, with and without the assumption that the mean values of the arms are increasing. In each case, we provide a lower bound valid for any risk $\delta$ and any $\delta$-correct algorithm; in addition, we propose an algorithm whose sample complexity is of the same order of magnitude for small risks. This work is motivated by phase 1 clinical trials, a practically important setting where the arm means are increasing by nature, and where no satisfactory solution is available so far.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge