Theory-Oriented Deep Leakage from Gradients via Linear Equation Solver

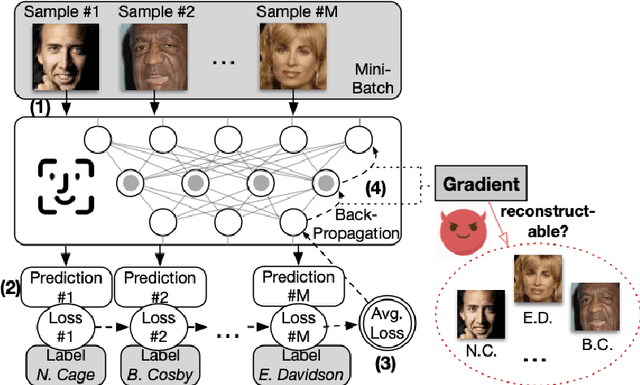
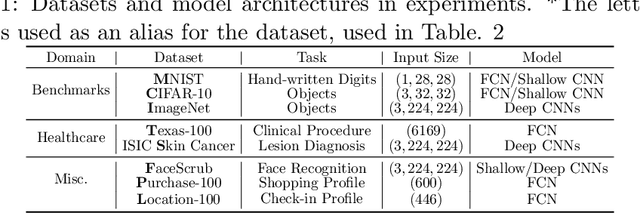
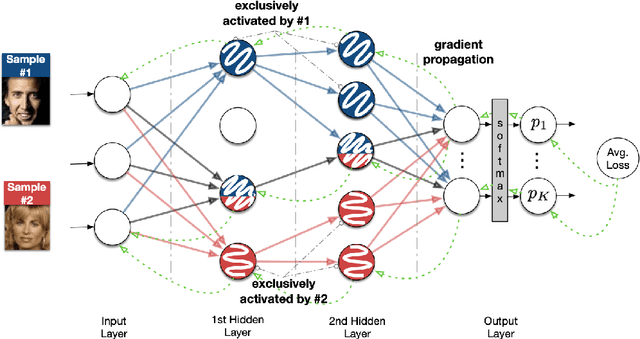
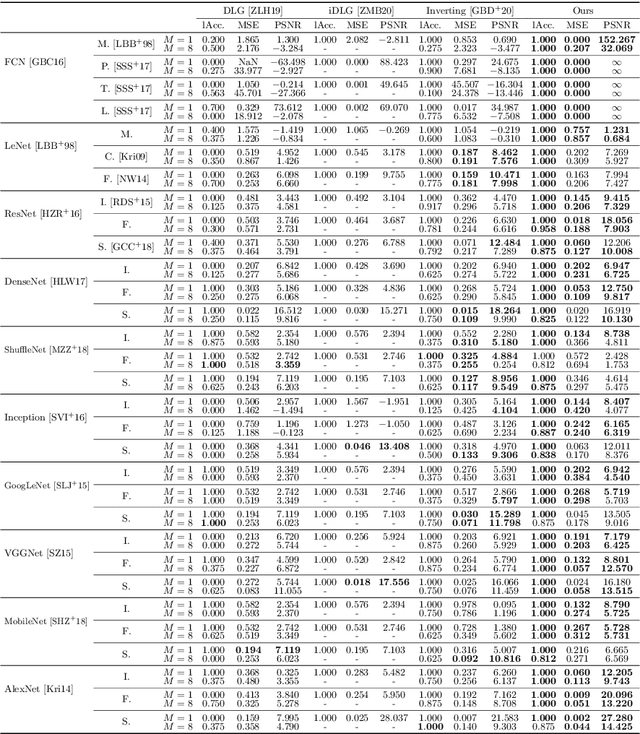
In this paper, we take a theory-oriented approach to systematically study the privacy properties of gradients from a broad class of neural networks with rectified linear units (ReLU), probably the most popular activation function used in current deep learning practices. By utilizing some intrinsic properties of neural networks with ReLU, we prove the existence of exclusively activated neurons is critical to the separability of the activation patterns of different samples. Intuitively, an activation pattern is like the fingerprint of the corresponding sample during the training process. With the separated activation patterns, we for the first time show the equivalence of data reconstruction attacks with a sparse linear equation system. In practice, we propose a novel data reconstruction attack on fully-connected neural networks and extend the attack to more commercial convolutional neural network architectures. Our systematic evaluations cover more than $10$ representative neural network architectures (e.g., GoogLeNet, VGGNet and $6$ more), on various real-world scenarios related with healthcare, medical imaging, location, face recognition and shopping behaviors. In the majority of test cases, our proposed attack is able to infer ground-truth labels in the training batch with near $100\%$ accuracy, reconstruct the input data to fully-connected neural networks with lower than $10^{-6}$ MSE error, and provide better reconstruction results on both shallow and deep convolutional neural networks than previous attacks.