Theoretical Limits of Pipeline Parallel Optimization and Application to Distributed Deep Learning
Paper and Code
Oct 11, 2019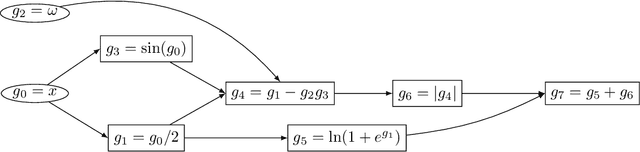
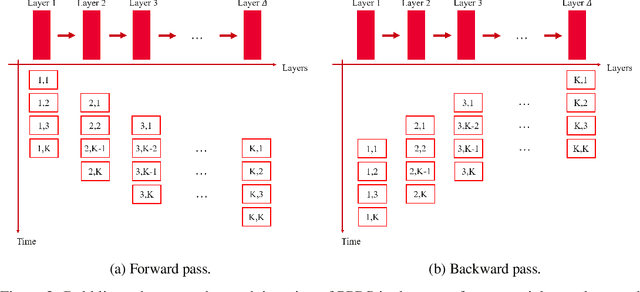
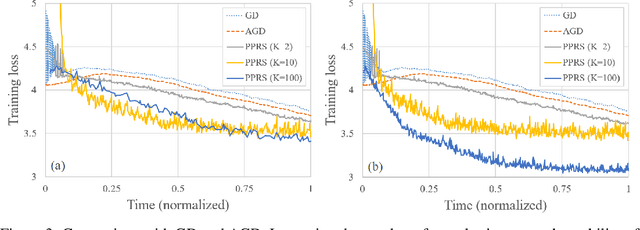
We investigate the theoretical limits of pipeline parallel learning of deep learning architectures, a distributed setup in which the computation is distributed per layer instead of per example. For smooth convex and non-convex objective functions, we provide matching lower and upper complexity bounds and show that a naive pipeline parallelization of Nesterov's accelerated gradient descent is optimal. For non-smooth convex functions, we provide a novel algorithm coined Pipeline Parallel Random Smoothing (PPRS) that is within a $d^{1/4}$ multiplicative factor of the optimal convergence rate, where $d$ is the underlying dimension. While the convergence rate still obeys a slow $\varepsilon^{-2}$ convergence rate, the depth-dependent part is accelerated, resulting in a near-linear speed-up and convergence time that only slightly depends on the depth of the deep learning architecture. Finally, we perform an empirical analysis of the non-smooth non-convex case and show that, for difficult and highly non-smooth problems, PPRS outperforms more traditional optimization algorithms such as gradient descent and Nesterov's accelerated gradient descent for problems where the sample size is limited, such as few-shot or adversarial learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge