Theoretical Evaluation of the Capacity-Achieving Distribution for IM-DD Fiber-Optic Channels
Paper and Code
Feb 23, 2023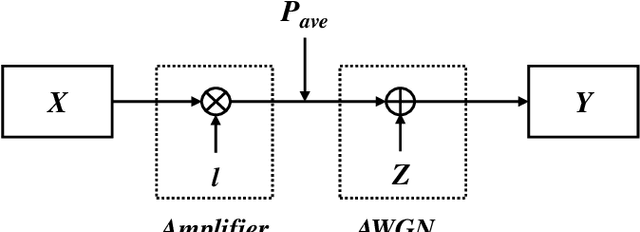
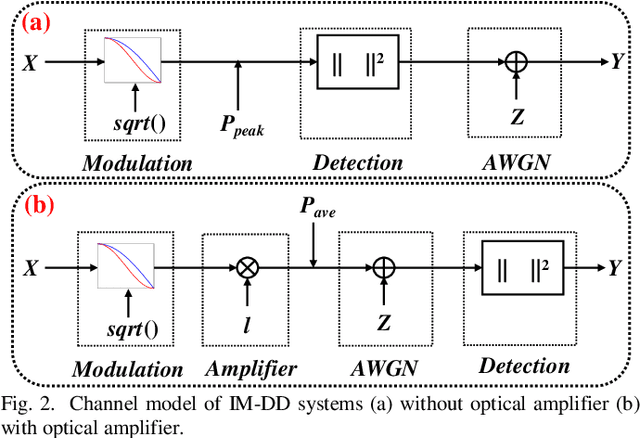
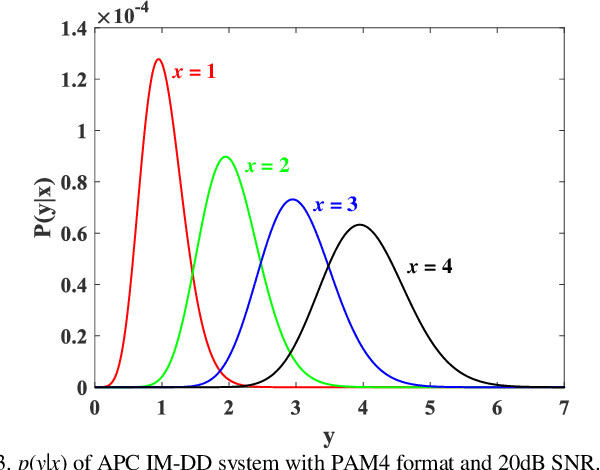
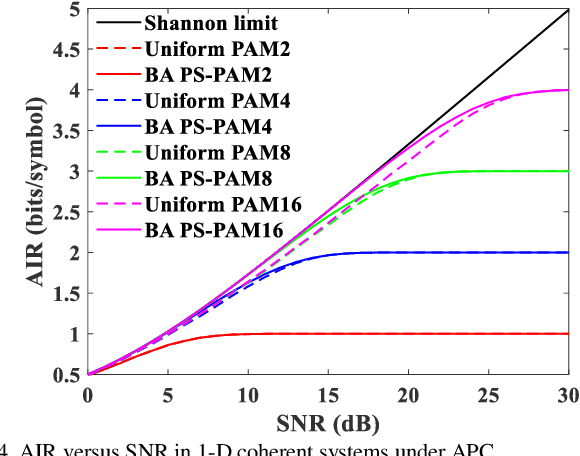
The capacity and capacity-achieving distribution for intensity-modulation and direct-detection (IM-DD) fiber-optic channels is theoretically investigated. Different from coherent fiber-optic channels, we indicate that the capacity-achieving distribution of IM-DD systems should be discussed separately in two cases: 1) IM-DD systems without optical amplifier, which are constrained in peak power; 2) IM-DD systems with optical amplifier, which are the average power constraint (APC) system. For the two models, the maximum mutual information achieving distribution, instead of the maximum input entropy achieving distribution, is numerically computed by the iterative Blahut-Arimoto (BA) algorithm. For the IM-DD system under peak power constraint (PPC), a dynamic-assignment BA algorithm is applied to find the capacity-achieving distribution with minimum cardinality. It is observed that the maximum difference between the minimum input cardinality and capacity is around 0.8 bits. For a fixed support input cardinality, although the observed shaping gain is small and only appears in low peak-signal-to-noise ratio (PSNR) regions in the PPC IM-DD system, the probabilistic shaping technique can also be used to introduce rate adaptation to the system by adjusting the shaping and FEC overheads since the capacity-achieving distribution is symmetric. In the IM-DD system under APC, a modified BA algorithm is investigated to solve for the capacity and capacity-achieving distribution, and a significant shaping gain is observed. For PAM8 and PAM16 modulation formats, 0.294 bits/symbol and 0.531 bits/symbol shaping gain can be obtained at the SNR of 20dB. Furthermore, since the capacity-achieving distribution is asymmetric in this case, a practical discussion of the PS technique is also presented.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge