The Role of Linear Layers in Nonlinear Interpolating Networks
Paper and Code
Feb 02, 2022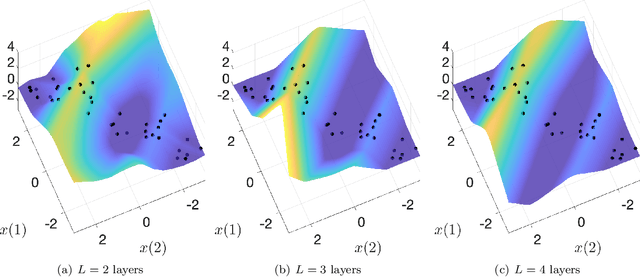
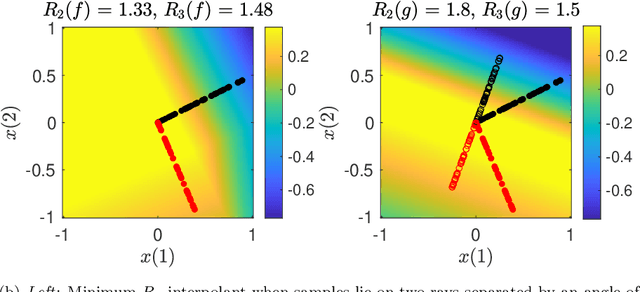
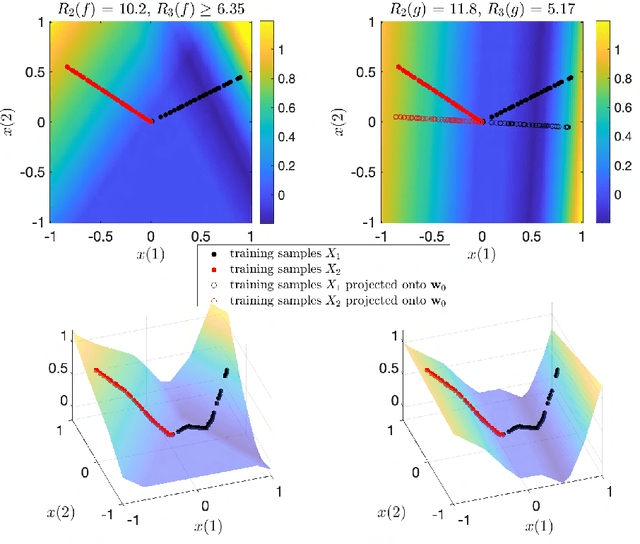
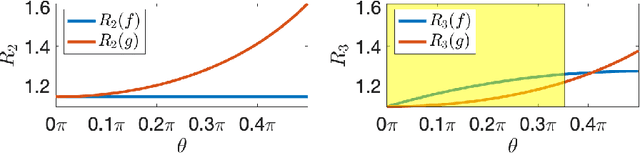
This paper explores the implicit bias of overparameterized neural networks of depth greater than two layers. Our framework considers a family of networks of varying depth that all have the same capacity but different implicitly defined representation costs. The representation cost of a function induced by a neural network architecture is the minimum sum of squared weights needed for the network to represent the function; it reflects the function space bias associated with the architecture. Our results show that adding linear layers to a ReLU network yields a representation cost that reflects a complex interplay between the alignment and sparsity of ReLU units. Specifically, using a neural network to fit training data with minimum representation cost yields an interpolating function that is constant in directions perpendicular to a low-dimensional subspace on which a parsimonious interpolant exists.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge