The Responsibility Weighted Mahalanobis Kernel for Semi-Supervised Training of Support Vector Machines for Classification
Paper and Code
Feb 16, 2015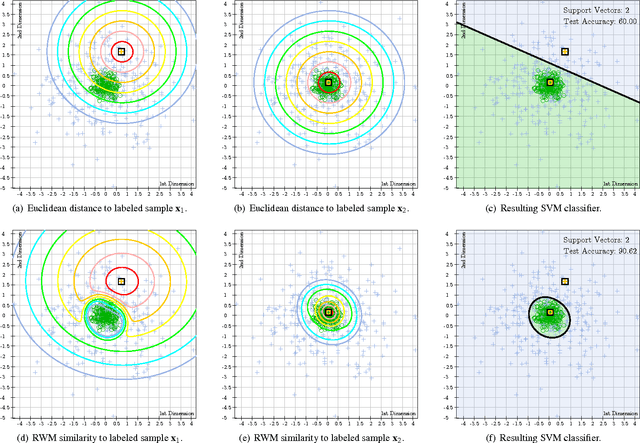
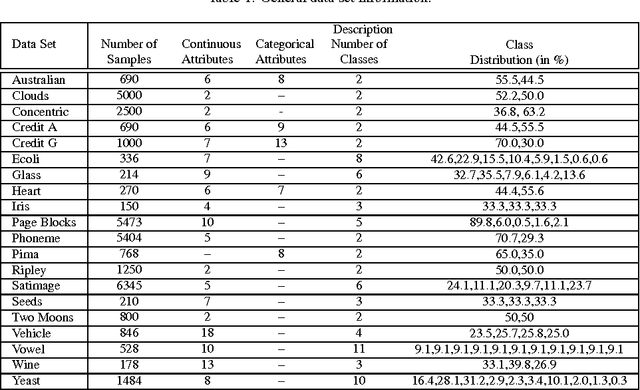
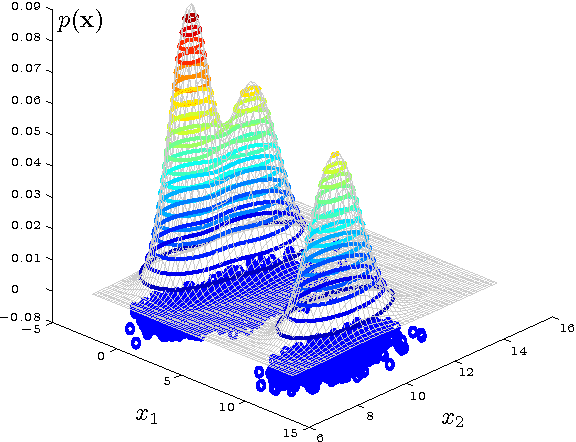
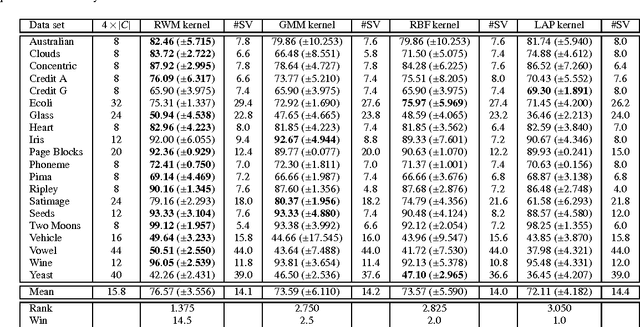
Kernel functions in support vector machines (SVM) are needed to assess the similarity of input samples in order to classify these samples, for instance. Besides standard kernels such as Gaussian (i.e., radial basis function, RBF) or polynomial kernels, there are also specific kernels tailored to consider structure in the data for similarity assessment. In this article, we will capture structure in data by means of probabilistic mixture density models, for example Gaussian mixtures in the case of real-valued input spaces. From the distance measures that are inherently contained in these models, e.g., Mahalanobis distances in the case of Gaussian mixtures, we derive a new kernel, the responsibility weighted Mahalanobis (RWM) kernel. Basically, this kernel emphasizes the influence of model components from which any two samples that are compared are assumed to originate (that is, the "responsible" model components). We will see that this kernel outperforms the RBF kernel and other kernels capturing structure in data (such as the LAP kernel in Laplacian SVM) in many applications where partially labeled data are available, i.e., for semi-supervised training of SVM. Other key advantages are that the RWM kernel can easily be used with standard SVM implementations and training algorithms such as sequential minimal optimization, and heuristics known for the parametrization of RBF kernels in a C-SVM can easily be transferred to this new kernel. Properties of the RWM kernel are demonstrated with 20 benchmark data sets and an increasing percentage of labeled samples in the training data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge