The quadratic Wasserstein metric for inverse data matching
Paper and Code
Nov 24, 2019
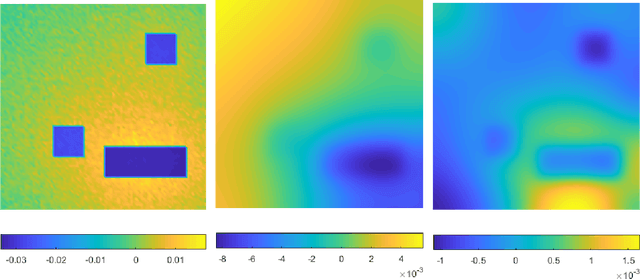
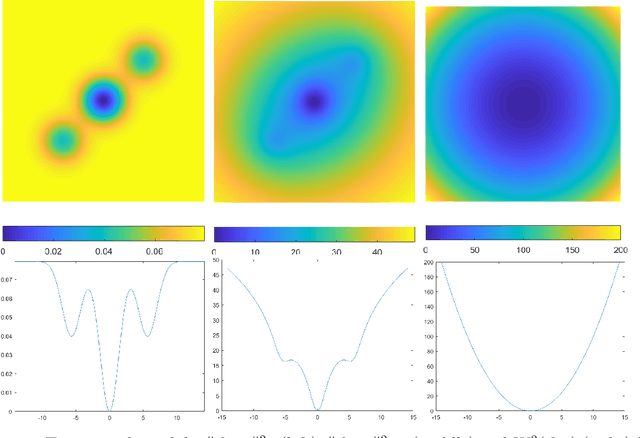
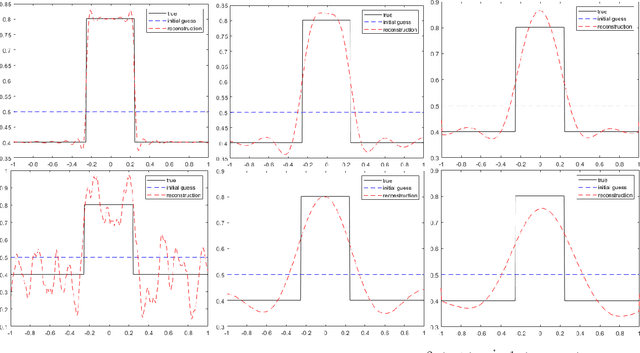
This work characterizes, analytically and numerically, two major effects of the quadratic Wasserstein ($W_2$) distance as the measure of data discrepancy in computational solutions of inverse problems. First, we show, in the infinite-dimensional setup, that the $W_2$ distance has a smoothing effect on the inversion process, making it robust against high-frequency noise in the data but leading to a reduced resolution for the reconstructed objects at a given noise level. Second, we demonstrate that for some finite-dimensional problems, the $W_2$ distance leads to optimization problems that have better convexity than the classical $L^2$ and $\dot{\mathcal{H}}^{-1}$ distances, making it a more preferred distance to use when solving such inverse matching problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge