The PAV algorithm optimizes binary proper scoring rules
Paper and Code
Apr 08, 2013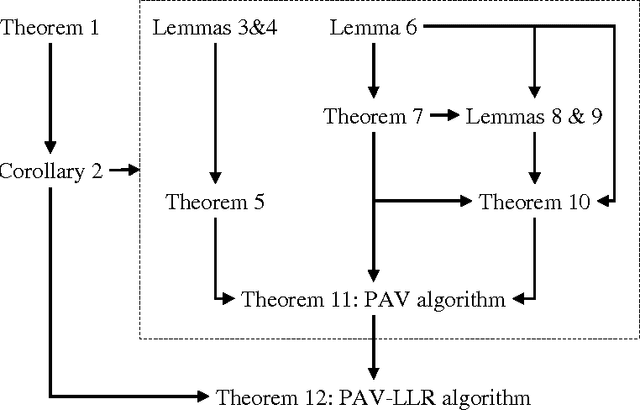
There has been much recent interest in application of the pool-adjacent-violators (PAV) algorithm for the purpose of calibrating the probabilistic outputs of automatic pattern recognition and machine learning algorithms. Special cost functions, known as proper scoring rules form natural objective functions to judge the goodness of such calibration. We show that for binary pattern classifiers, the non-parametric optimization of calibration, subject to a monotonicity constraint, can be solved by PAV and that this solution is optimal for all regular binary proper scoring rules. This extends previous results which were limited to convex binary proper scoring rules. We further show that this result holds not only for calibration of probabilities, but also for calibration of log-likelihood-ratios, in which case optimality holds independently of the prior probabilities of the pattern classes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge