The Pareto Frontier of Instance-Dependent Guarantees in Multi-Player Multi-Armed Bandits with no Communication
Paper and Code
Feb 19, 2022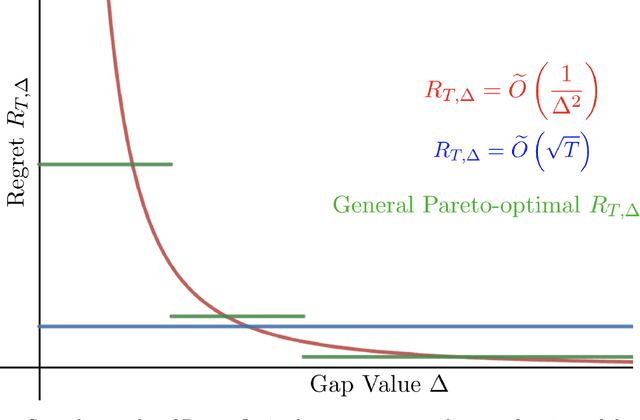
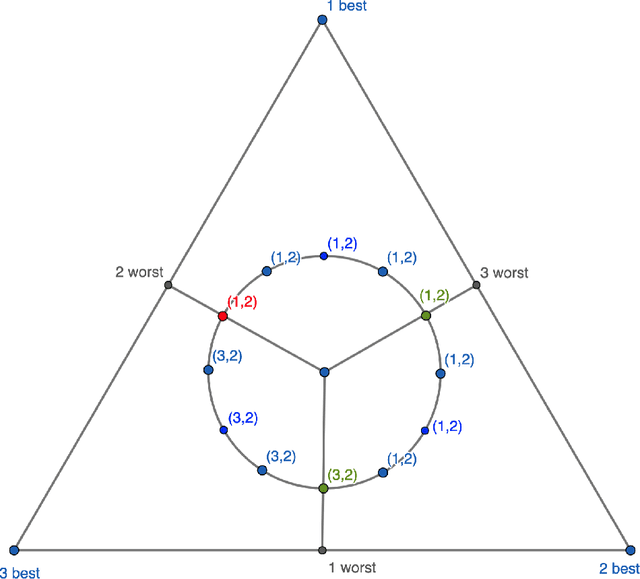
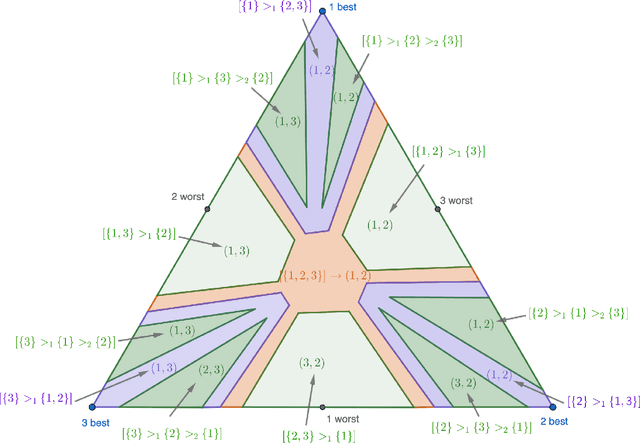
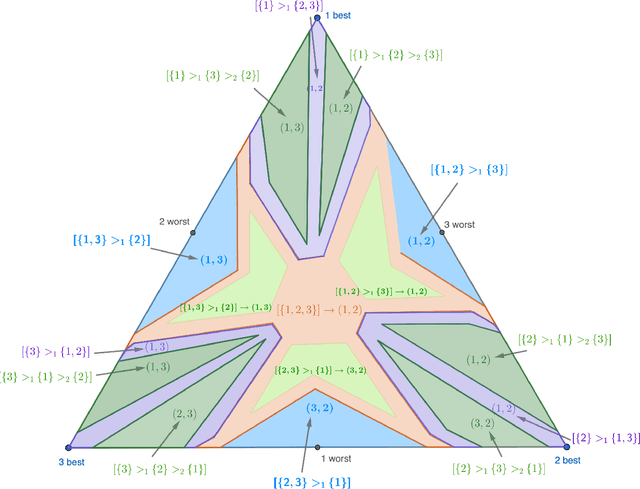
We study the stochastic multi-player multi-armed bandit problem. In this problem, $m$ players cooperate to maximize their total reward from $K > m$ arms. However the players cannot communicate and are penalized (e.g. receive no reward) if they pull the same arm at the same time. We ask whether it is possible to obtain optimal instance-dependent regret $\tilde{O}(1/\Delta)$ where $\Delta$ is the gap between the $m$-th and $m+1$-st best arms. Such guarantees were recently achieved in a model allowing the players to implicitly communicate through intentional collisions. We show that with no communication at all, such guarantees are, surprisingly, not achievable. In fact, obtaining the optimal $\tilde{O}(1/\Delta)$ regret for some regimes of $\Delta$ necessarily implies strictly sub-optimal regret in other regimes. Our main result is a complete characterization of the Pareto optimal instance-dependent trade-offs that are possible with no communication. Our algorithm generalizes that of Bubeck, Budzinski, and the second author and enjoys the same strong no-collision property, while our lower bound is based on a topological obstruction and holds even under full information.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge