The multilayer random dot product graph

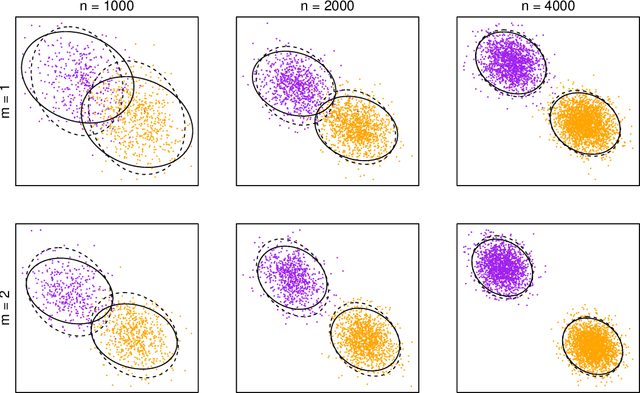
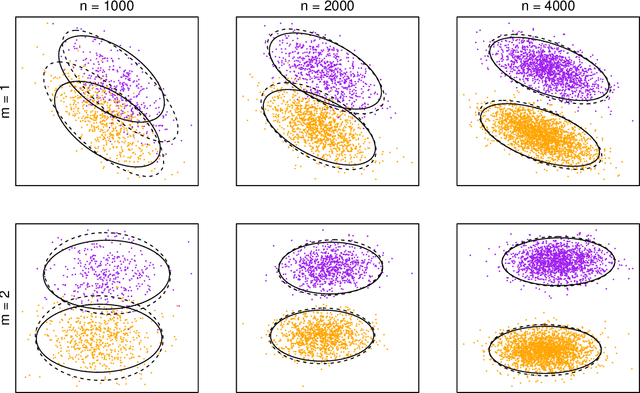
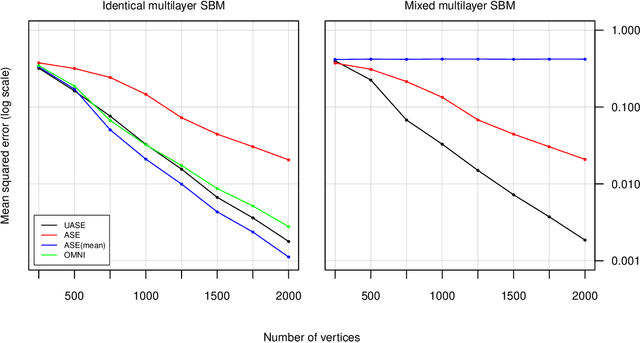
We present an extension of the latent position network model known as the generalised random dot product graph to accommodate multiple graphs with a common node structure, based on a matrix representation of the natural third-order tensor created from the adjacency matrices of these graphs. Theoretical results concerning the asymptotic behaviour of the node representations obtained by spectral embedding are established, showing that after the application of a linear transformation these converge uniformly in the Euclidean norm to the latent positions with a Gaussian error. The flexibility of the model is demonstrated through application to the tasks of latent position recovery and two-graph hypothesis testing, in which it performs favourably compared to existing models. Empirical improvements in link prediction over single graph embeddings are exhibited in a cyber-security example.