The iterative reweighted Mixed-Norm Estimate for spatio-temporal MEG/EEG source reconstruction
Paper and Code
Jul 28, 2016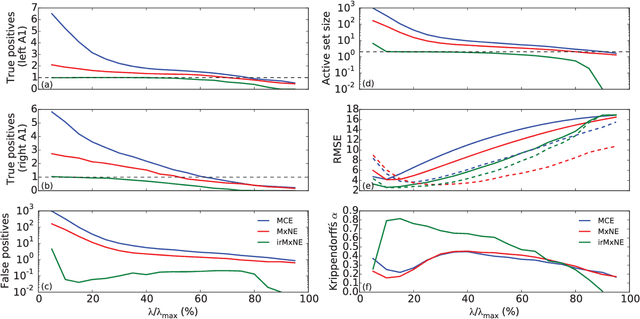
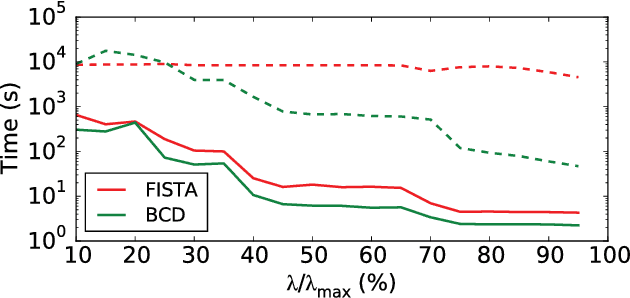
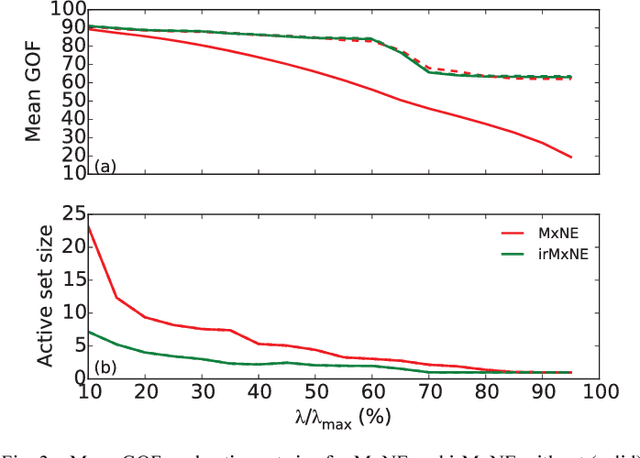
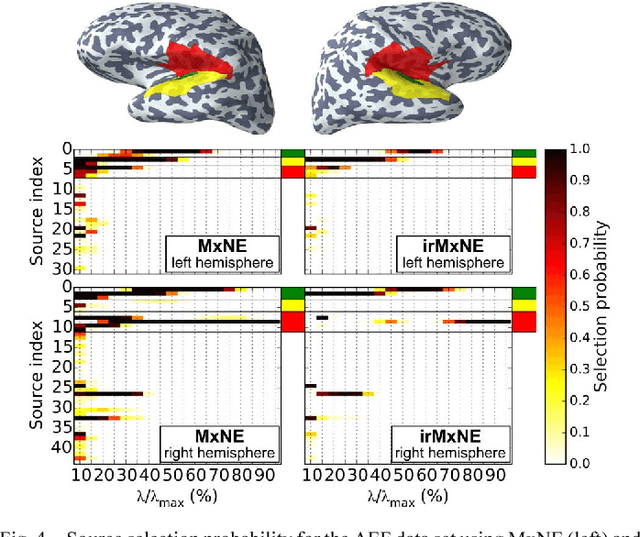
Source imaging based on magnetoencephalography (MEG) and electroencephalography (EEG) allows for the non-invasive analysis of brain activity with high temporal and good spatial resolution. As the bioelectromagnetic inverse problem is ill-posed, constraints are required. For the analysis of evoked brain activity, spatial sparsity of the neuronal activation is a common assumption. It is often taken into account using convex constraints based on the l1-norm. The resulting source estimates are however biased in amplitude and often suboptimal in terms of source selection due to high correlations in the forward model. In this work, we demonstrate that an inverse solver based on a block-separable penalty with a Frobenius norm per block and a l0.5-quasinorm over blocks addresses both of these issues. For solving the resulting non-convex optimization problem, we propose the iterative reweighted Mixed Norm Estimate (irMxNE), an optimization scheme based on iterative reweighted convex surrogate optimization problems, which are solved efficiently using a block coordinate descent scheme and an active set strategy. We compare the proposed sparse imaging method to the dSPM and the RAP-MUSIC approach based on two MEG data sets. We provide empirical evidence based on simulations and analysis of MEG data that the proposed method improves on the standard Mixed Norm Estimate (MxNE) in terms of amplitude bias, support recovery, and stability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge