The Interpolation Phase Transition in Neural Networks: Memorization and Generalization under Lazy Training

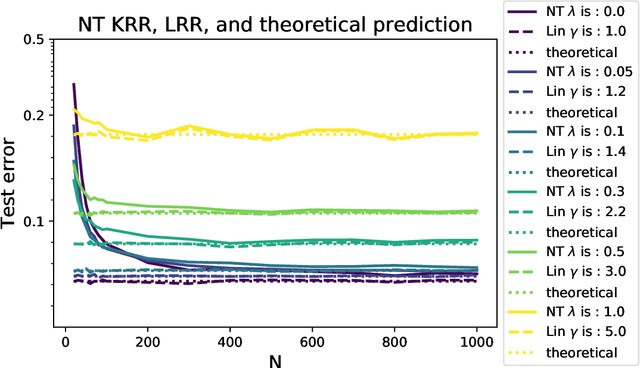
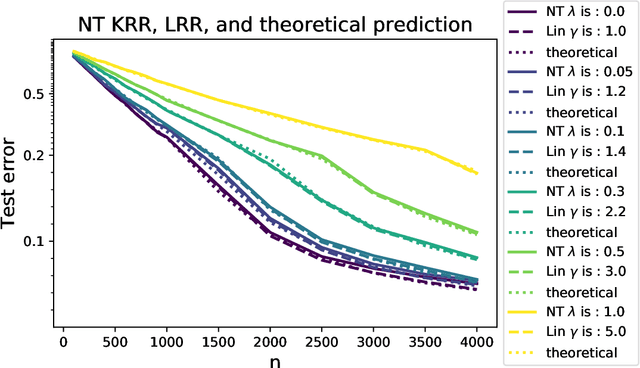
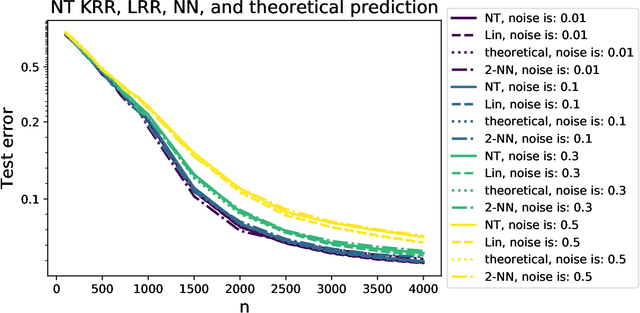
Modern neural networks are often operated in a strongly overparametrized regime: they comprise so many parameters that they can interpolate the training set, even if actual labels are replaced by purely random ones. Despite this, they achieve good prediction error on unseen data: interpolating the training set does not induce overfitting. Further, overparametrization appears to be beneficial in that it simplifies the optimization landscape. Here we study these phenomena in the context of two-layers neural networks in the neural tangent (NT) regime. We consider a simple data model, with isotropic feature vectors in $d$ dimensions, and $N$ hidden neurons. Under the assumption $N \le Cd$ (for $C$ a constant), we show that the network can exactly interpolate the data as soon as the number of parameters is significantly larger than the number of samples: $Nd\gg n$. Under these assumptions, we show that the empirical NT kernel has minimum eigenvalue bounded away from zero, and characterize the generalization error of min-$\ell_2$ norm interpolants, when the target function is linear. In particular, we show that the network approximately performs ridge regression in the raw features, with a strictly positive `self-induced' regularization.