The Generalized Traveling Salesman Problem solved with Ant Algorithms
Paper and Code
Oct 09, 2013
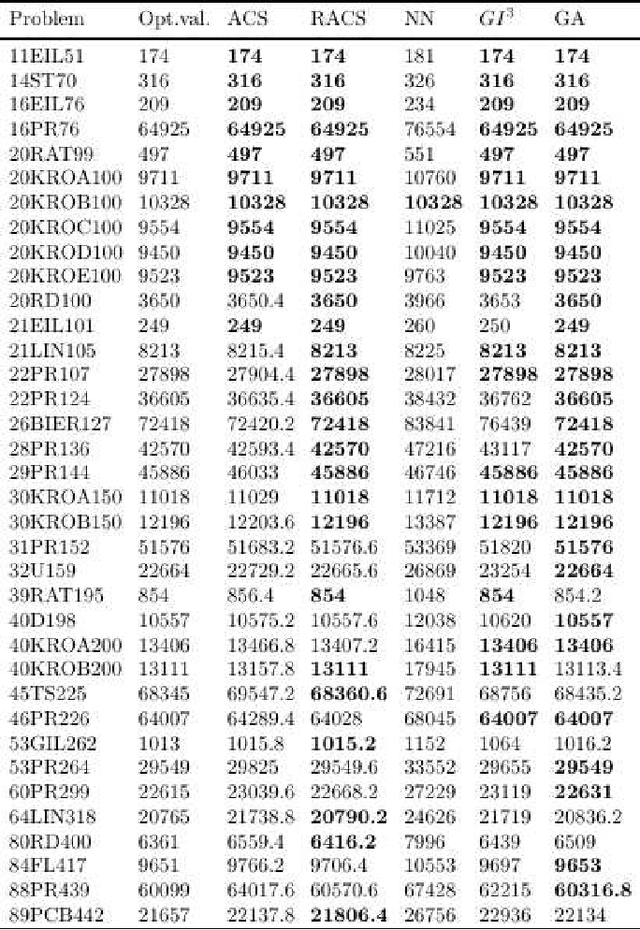
A well known N P-hard problem called the Generalized Traveling Salesman Problem (GTSP) is considered. In GTSP the nodes of a complete undirected graph are partitioned into clusters. The objective is to find a minimum cost tour passing through exactly one node from each cluster. An exact exponential time algorithm and an effective meta-heuristic algorithm for the problem are presented. The meta-heuristic proposed is a modified Ant Colony System (ACS) algorithm called Reinforcing Ant Colony System (RACS) which introduces new correction rules in the ACS algorithm. Computational results are reported for many standard test problems. The proposed algorithm is competitive with the other already proposed heuristics for the GTSP in both solution quality and computational time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge