The Generalized Eigenvalue Problem as a Nash Equilibrium

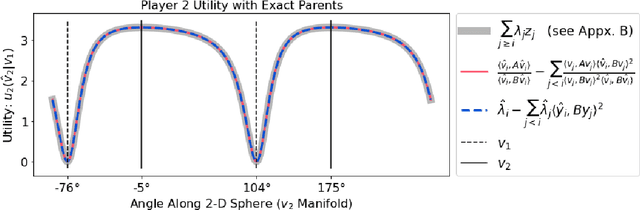
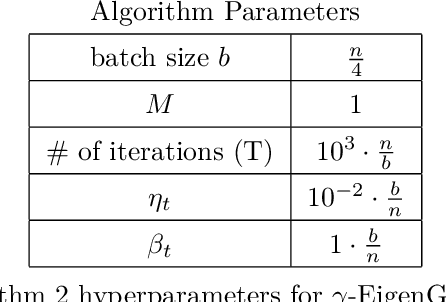
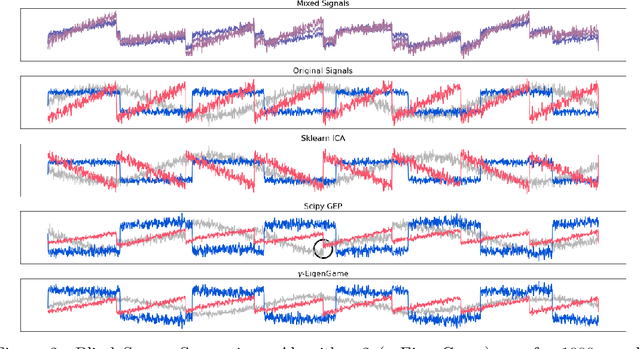
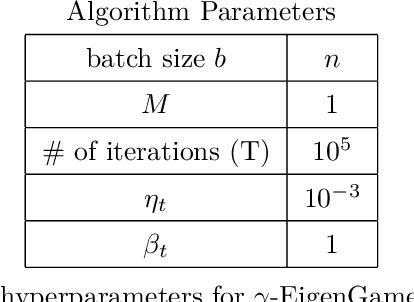
The generalized eigenvalue problem (GEP) is a fundamental concept in numerical linear algebra. It captures the solution of many classical machine learning problems such as canonical correlation analysis, independent components analysis, partial least squares, linear discriminant analysis, principal components, successor features and others. Despite this, most general solvers are prohibitively expensive when dealing with massive data sets and research has instead concentrated on finding efficient solutions to specific problem instances. In this work, we develop a game-theoretic formulation of the top-$k$ GEP whose Nash equilibrium is the set of generalized eigenvectors. We also present a parallelizable algorithm with guaranteed asymptotic convergence to the Nash. Current state-of-the-art methods require $\mathcal{O}(d^2k)$ complexity per iteration which is prohibitively expensive when the number of dimensions ($d$) is large. We show how to achieve $\mathcal{O}(dk)$ complexity, scaling to datasets $100\times$ larger than those evaluated by prior methods. Empirically we demonstrate that our algorithm is able to solve a variety of GEP problem instances including a large-scale analysis of neural network activations.