The Expected Jacobian Outerproduct: Theory and Empirics
Paper and Code
Jun 05, 2020
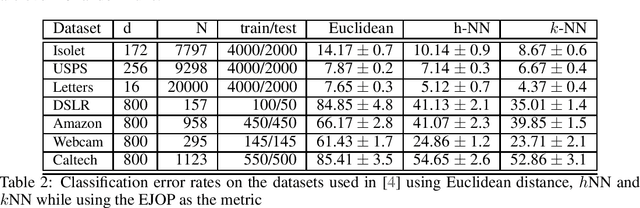
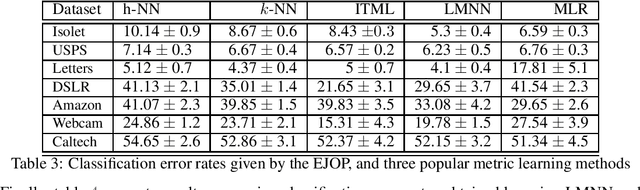
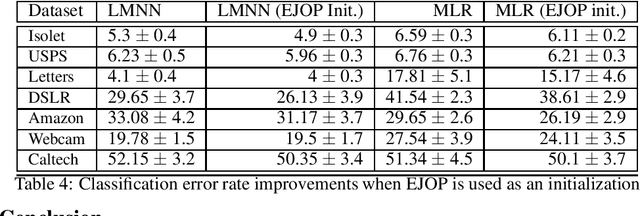
The expected gradient outerproduct (EGOP) of an unknown regression function is an operator that arises in the theory of multi-index regression, and is known to recover those directions that are most relevant to predicting the output. However, work on the EGOP, including that on its cheap estimators, is restricted to the regression setting. In this work, we adapt this operator to the multi-class setting, which we dub the expected Jacobian outerproduct (EJOP). Moreover, we propose a simple rough estimator of the EJOP and show that somewhat surprisingly, it remains statistically consistent under mild assumptions. Furthermore, we show that the eigenvalues and eigenspaces also remain consistent. Finally, we show that the estimated EJOP can be used as a metric to yield improvements in real-world non-parametric classification tasks: both by its use as a metric, and also as cheap initialization in metric learning tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge