The efficacy and generalizability of conditional GANs for posterior inference in physics-based inverse problems
Paper and Code
Feb 15, 2022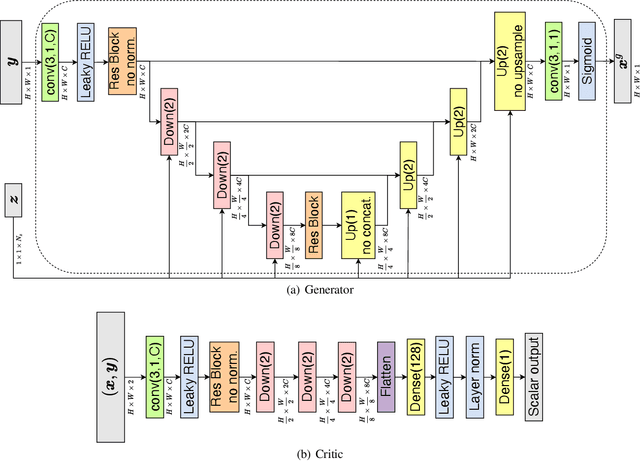
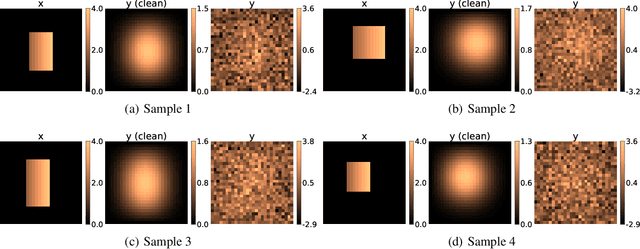
In this work, we train conditional Wasserstein generative adversarial networks to effectively sample from the posterior of physics-based Bayesian inference problems. The generator is constructed using a U-Net architecture, with the latent information injected using conditional instance normalization. The former facilitates a multiscale inverse map, while the latter enables the decoupling of the latent space dimension from the dimension of the measurement, and introduces stochasticity at all scales of the U-Net. We solve PDE-based inverse problems to demonstrate the performance of our approach in quantifying the uncertainty in the inferred field. Further, we show the generator can learn inverse maps which are local in nature, which in turn promotes generalizability when testing with out-of-distribution samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge