The effect of measurement error on clustering algorithms
Paper and Code
May 24, 2020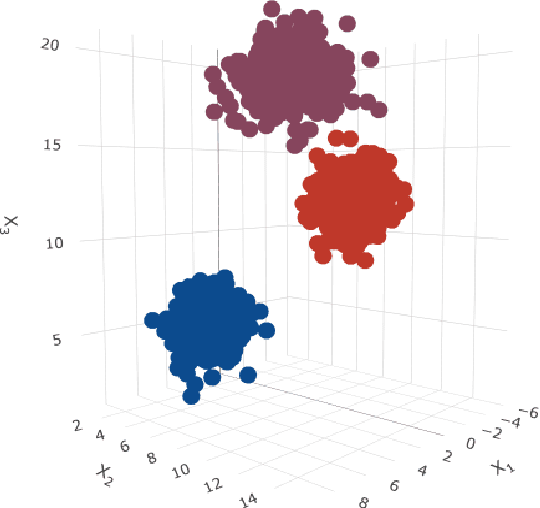
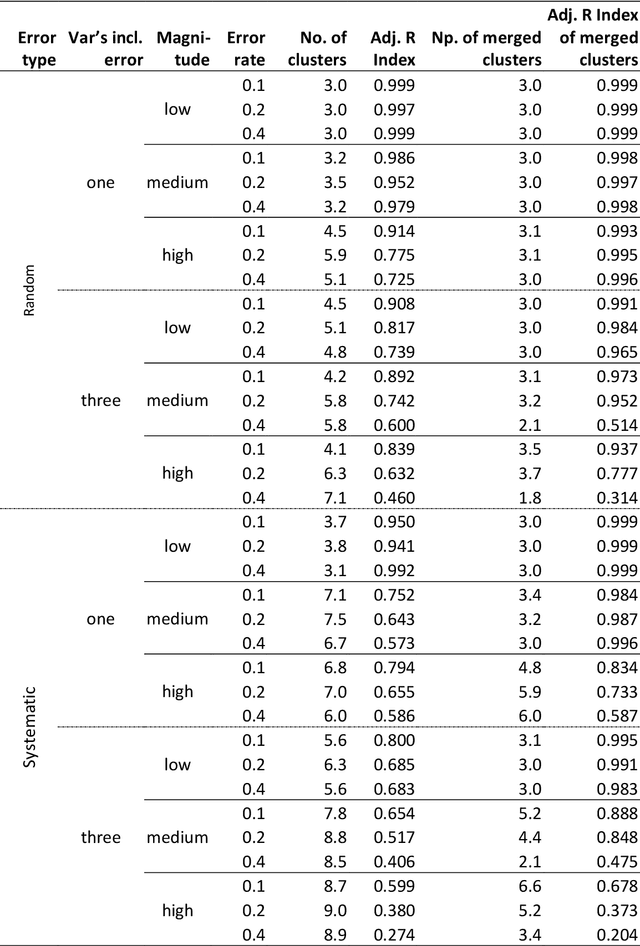
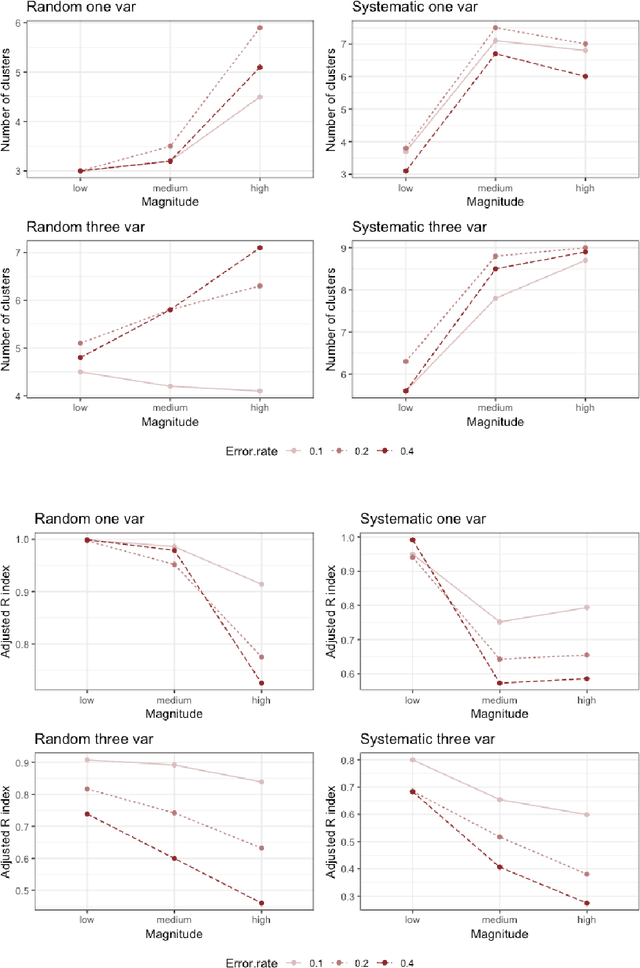

Clustering consists of a popular set of techniques used to separate data into interesting groups for further analysis. Many data sources on which clustering is performed are well-known to contain random and systematic measurement errors. Such errors may adversely affect clustering. While several techniques have been developed to deal with this problem, little is known about the effectiveness of these solutions. Moreover, no work to-date has examined the effect of systematic errors on clustering solutions. In this paper, we perform a Monte Carlo study to investigate the sensitivity of two common clustering algorithms, GMMs with merging and DBSCAN, to random and systematic error. We find that measurement error is particularly problematic when it is systematic and when it affects all variables in the dataset. For the conditions considered here, we also find that the partition-based GMM with merged components is less sensitive to measurement error than the density-based DBSCAN procedure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge