The dynamics of learning with feedback alignment

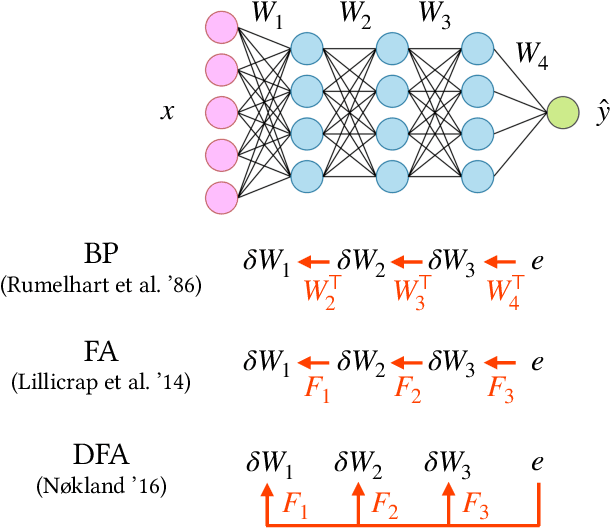
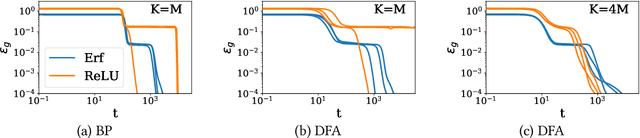
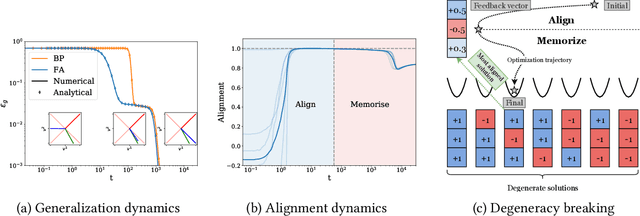
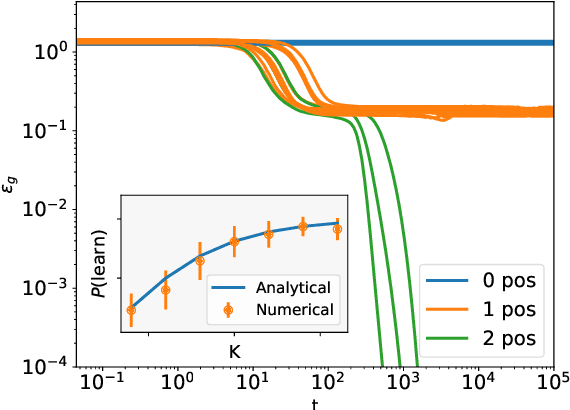
Direct Feedback Alignment (DFA) is emerging as an efficient and biologically plausible alternative to the ubiquitous backpropagation algorithm for training deep neural networks. Despite relying on random feedback weights for the backward pass, DFA successfully trains state-of-the-art models such as Transformers. On the other hand, it notoriously fails to train convolutional networks. An understanding of the inner workings of DFA to explain these diverging results remains elusive. Here, we propose a theory for the success of DFA. We first show that learning in shallow networks proceeds in two steps: an alignment phase, where the model adapts its weights to align the approximate gradient with the true gradient of the loss function, is followed by a memorisation phase, where the model focuses on fitting the data. This two-step process has a degeneracy breaking effect: out of all the low-loss solutions in the landscape, a network trained with DFA naturally converges to the solution which maximises gradient alignment. We also identify a key quantity underlying alignment in deep linear networks: the conditioning of the alignment matrices. The latter enables a detailed understanding of the impact of data structure on alignment, and suggests a simple explanation for the well-known failure of DFA to train convolutional neural networks. Numerical experiments on MNIST and CIFAR10 clearly demonstrate degeneracy breaking in deep non-linear networks and show that the align-then-memorize process occurs sequentially from the bottom layers of the network to the top.