The Diverse Cohort Selection Problem

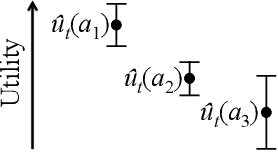
How should a firm allocate its limited interviewing resources to select the optimal cohort of new employees from a large set of job applicants? How should that firm allocate cheap but noisy resume screenings and expensive but in-depth in-person interviews? We view this problem through the lens of combinatorial pure exploration (CPE) in the multi-armed bandit setting, where a central learning agent performs costly exploration of a set of arms before selecting a final subset with some combinatorial structure. We generalize a recent CPE algorithm to the setting where arm pulls can have different costs, and return different levels of information, and prove theoretical upper bounds for a general class of arm-pulling strategies in this new setting. We then apply our general algorithm to a real-world problem with combinatorial structure: incorporating diversity into university admissions. We take real data from admissions at one of the largest US-based computer science graduate programs and show that a simulation of our algorithm produces more diverse student cohorts at low cost to individual student quality, spending comparable budget to the current admissions process at that university.