The DEformer: An Order-Agnostic Distribution Estimating Transformer
Paper and Code
Jul 11, 2021
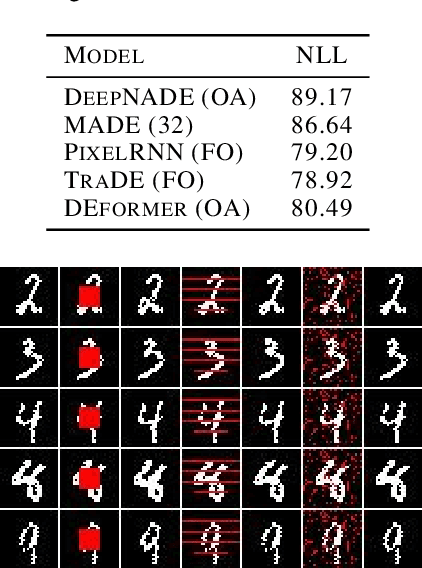

Order-agnostic autoregressive distribution (density) estimation (OADE), i.e., autoregressive distribution estimation where the features can occur in an arbitrary order, is a challenging problem in generative machine learning. Prior work on OADE has encoded feature identity by assigning each feature to a distinct fixed position in an input vector. As a result, architectures built for these inputs must strategically mask either the input or model weights to learn the various conditional distributions necessary for inferring the full joint distribution of the dataset in an order-agnostic way. In this paper, we propose an alternative approach for encoding feature identities, where each feature's identity is included alongside its value in the input. This feature identity encoding strategy allows neural architectures designed for sequential data to be applied to the OADE task without modification. As a proof of concept, we show that a Transformer trained on this input (which we refer to as "the DEformer", i.e., the distribution estimating Transformer) can effectively model binarized-MNIST, approaching the performance of fixed-order autoregressive distribution estimating algorithms while still being entirely order-agnostic. Additionally, we find that the DEformer surpasses the performance of recent flow-based architectures when modeling a tabular dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge