The Benefit of Sex in Noisy Evolutionary Search

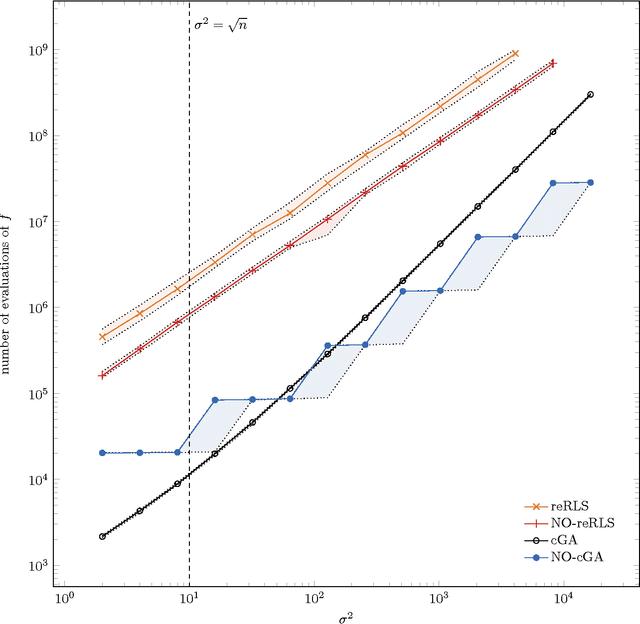
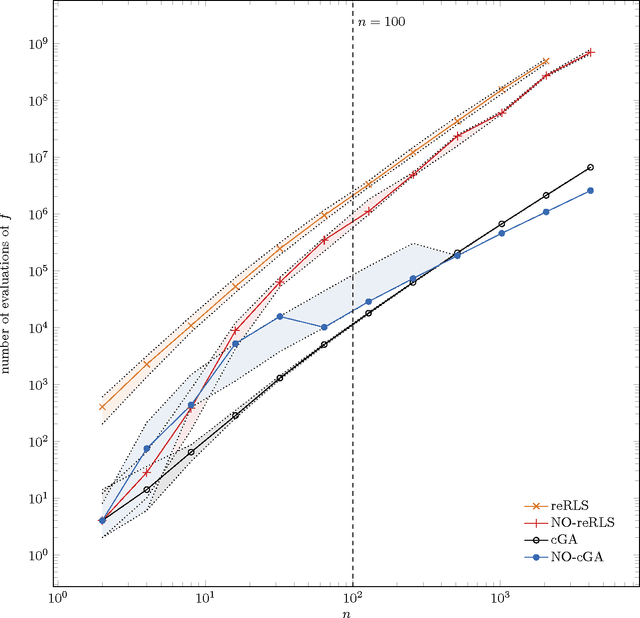
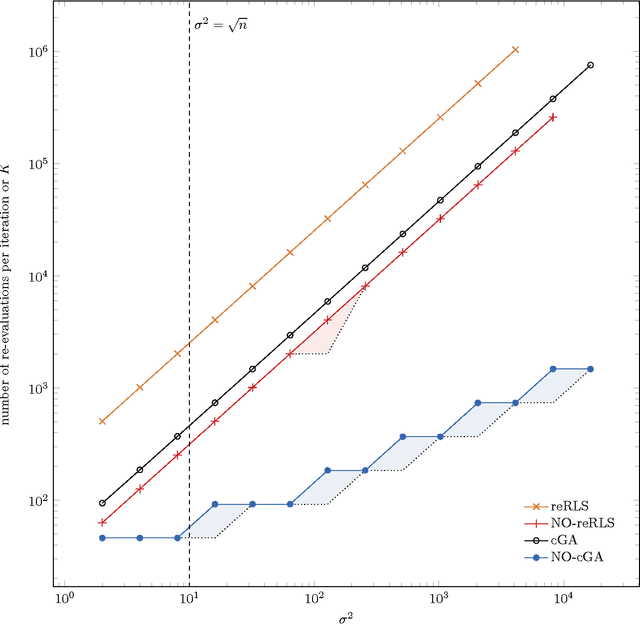
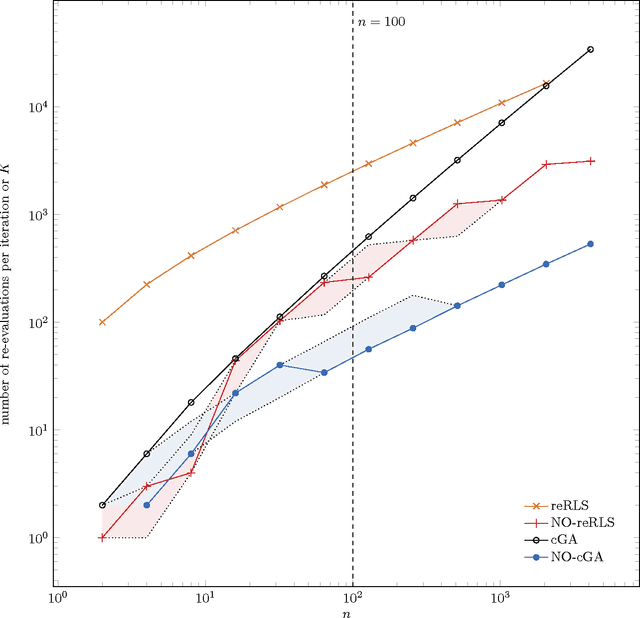
The benefit of sexual recombination is one of the most fundamental questions both in population genetics and evolutionary computation. It is widely believed that recombination helps solving difficult optimization problems. We present the first result, which rigorously proves that it is beneficial to use sexual recombination in an uncertain environment with a noisy fitness function. For this, we model sexual recombination with a simple estimation of distribution algorithm called the Compact Genetic Algorithm (cGA), which we compare with the classical $\mu+1$ EA. For a simple noisy fitness function with additive Gaussian posterior noise $\mathcal{N}(0,\sigma^2)$, we prove that the mutation-only $\mu+1$ EA typically cannot handle noise in polynomial time for $\sigma^2$ large enough while the cGA runs in polynomial time as long as the population size is not too small. This shows that in this uncertain environment sexual recombination is provably beneficial. We observe the same behavior in a small empirical study.