Tensorizing Subgraph Search in the Supernet

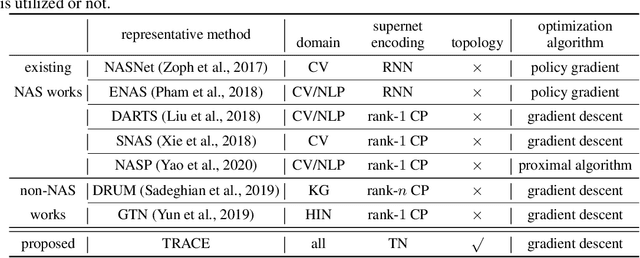
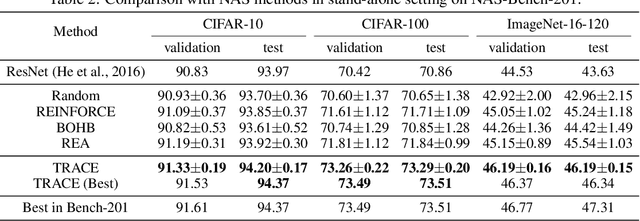
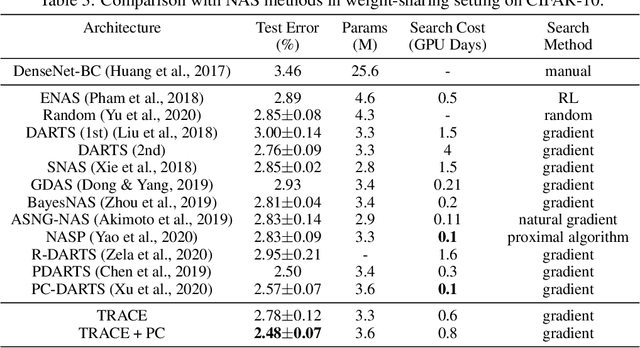
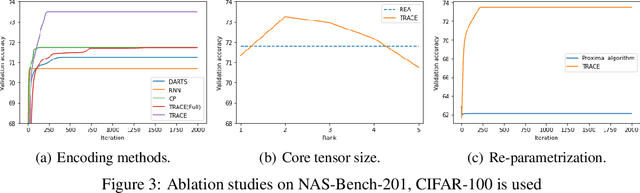
Recently, a special kind of graph, i.e., supernet, which allows two nodes connected by multi-choice edges, has exhibited its power in neural architecture search (NAS) by searching for better architectures for computer vision (CV) and natural language processing (NLP) tasks. In this paper, we discover that the design of such discrete architectures also appears in many other important learning tasks, e.g., logical chain inference in knowledge graphs (KGs) and meta-path discovery in heterogeneous information networks (HINs). Thus, we are motivated to generalize the supernet search problem on a broader horizon. However, none of the existing works are effective since the supernet topology is highly task-dependent and diverse. To address this issue, we propose to tensorize the supernet, i.e., unify the subgraph search problems by a tensor formulation and encode the topology inside the supernet by a tensor network. We further propose an efficient algorithm that admits both stochastic and deterministic objectives to solve the search problem. Finally, we perform extensive experiments on diverse learning tasks, i.e., architecture design for CV, logic inference for KG, and meta-path discovery for HIN. Empirical results demonstrate that our method leads to better performance and architectures.