Tensor Q-Rank: A New Data Dependent Tensor Rank

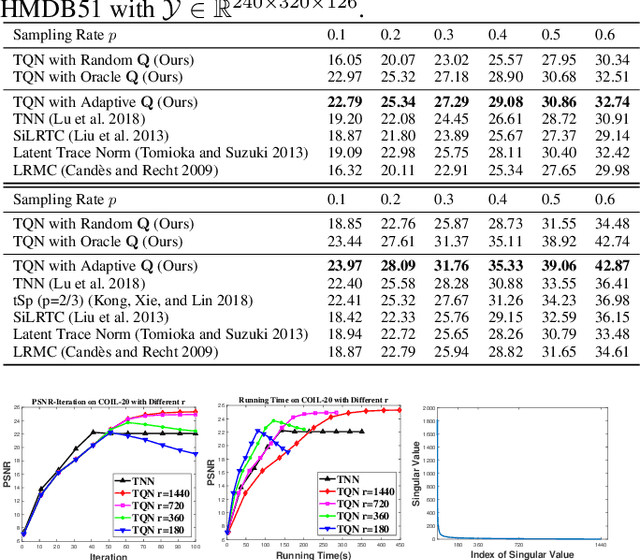
Recently, the \textit{Tensor Nuclear Norm~(TNN)} regularization based on t-SVD has been widely used in various low tubal-rank tensor recovery tasks. However, these models usually require smooth change of data along the third dimension to ensure their low rank structures. In this paper, we propose a new definition of tensor rank named \textit{tensor Q-rank} by a column orthonormal matrix $\mathbf{Q}$, and further make $\mathbf{Q}$ data-dependent. We introduce an explainable selection method of $\mathbf{Q}$, under which the data tensor may have a more significant low tensor Q-rank structure than that of low tubal-rank structure. We also provide a corresponding envelope of our rank function and apply it to the low rank tensor completion problem. Then we give an effective algorithm and briefly analyze why our method works better than TNN based methods in the case of complex data with low sampling rate. Finally, experimental results on real-world datasets demonstrate the superiority of our proposed model in the tensor completion problem.