Tensor Decompositions for Modeling Inverse Dynamics
Paper and Code
Nov 13, 2017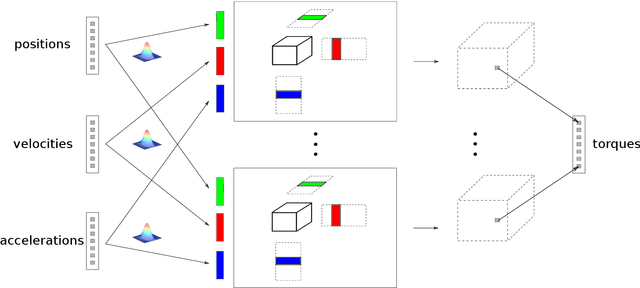

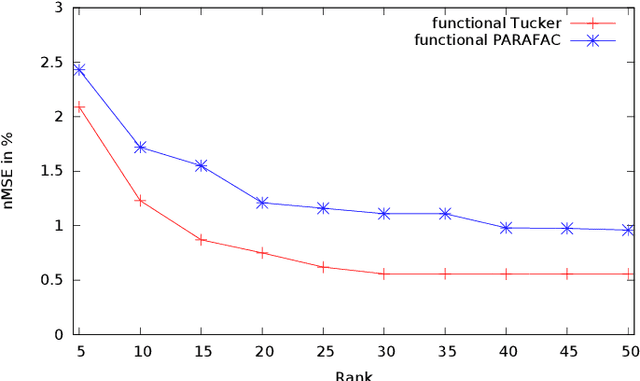
Modeling inverse dynamics is crucial for accurate feedforward robot control. The model computes the necessary joint torques, to perform a desired movement. The highly non-linear inverse function of the dynamical system can be approximated using regression techniques. We propose as regression method a tensor decomposition model that exploits the inherent three-way interaction of positions x velocities x accelerations. Most work in tensor factorization has addressed the decomposition of dense tensors. In this paper, we build upon the decomposition of sparse tensors, with only small amounts of nonzero entries. The decomposition of sparse tensors has successfully been used in relational learning, e.g., the modeling of large knowledge graphs. Recently, the approach has been extended to multi-class classification with discrete input variables. Representing the data in high dimensional sparse tensors enables the approximation of complex highly non-linear functions. In this paper we show how the decomposition of sparse tensors can be applied to regression problems. Furthermore, we extend the method to continuous inputs, by learning a mapping from the continuous inputs to the latent representations of the tensor decomposition, using basis functions. We evaluate our proposed model on a dataset with trajectories from a seven degrees of freedom SARCOS robot arm. Our experimental results show superior performance of the proposed functional tensor model, compared to challenging state-of-the art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge