Temporal Reasoning with Probabilities
Paper and Code
Mar 27, 2013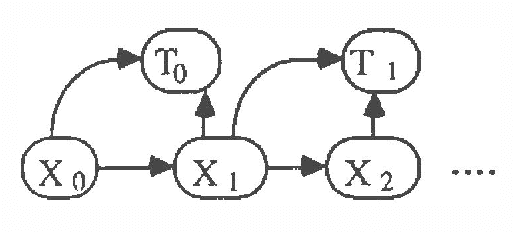
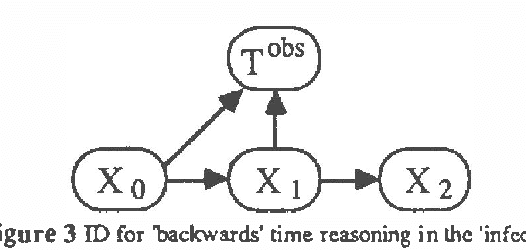
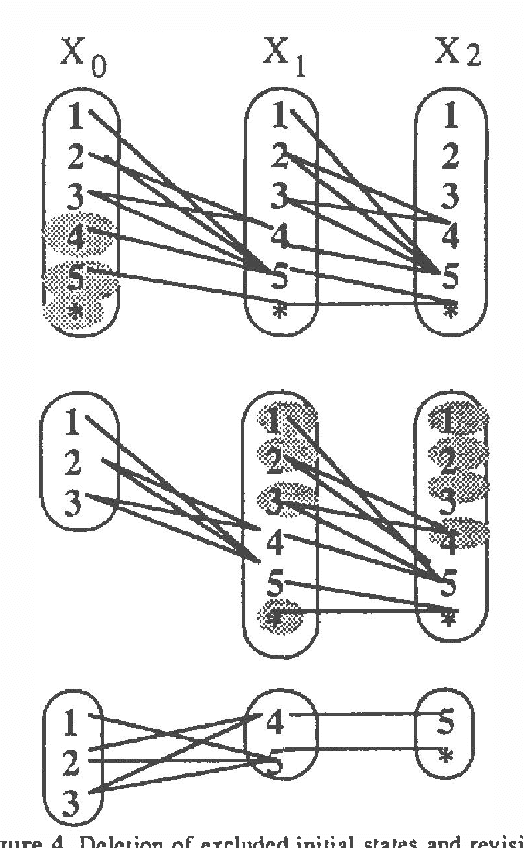

In this paper we explore representations of temporal knowledge based upon the formalism of Causal Probabilistic Networks (CPNs). Two different ?continuous-time? representations are proposed. In the first, the CPN includes variables representing ?event-occurrence times?, possibly on different time scales, and variables representing the ?state? of the system at these times. In the second, the CPN describes the influences between random variables with values in () representing dates, i.e. time-points associated with the occurrence of relevant events. However, structuring a system of inter-related dates as a network where all links commit to a single specific notion of cause and effect is in general far from trivial and leads to severe difficulties. We claim that we should recognize explicitly different kinds of relation between dates, such as ?cause?, ?inhibition?, ?competition?, etc., and propose a method whereby these relations are coherently embedded in a CPN using additional auxiliary nodes corresponding to "instrumental" variables. Also discussed, though not covered in detail, is the topic concerning how the quantitative specifications to be inserted in a temporal CPN can be learned from specific data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge