Taming the Long Tail of Deep Probabilistic Forecasting
Paper and Code
Mar 02, 2022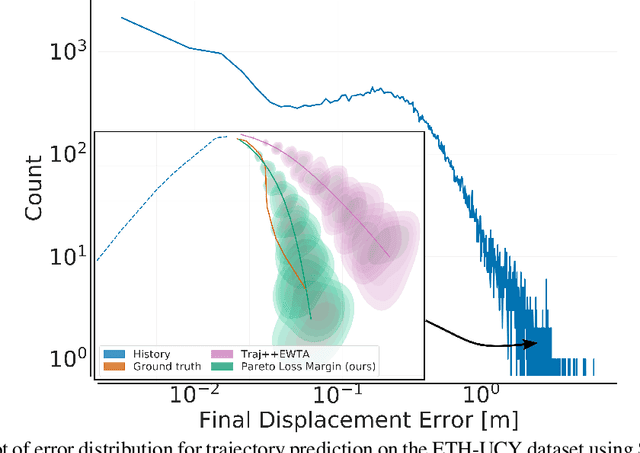
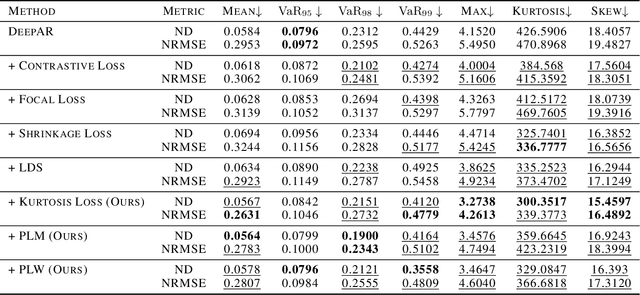

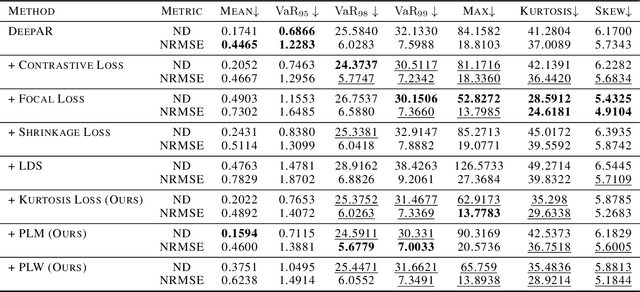
Deep probabilistic forecasting is gaining attention in numerous applications ranging from weather prognosis, through electricity consumption estimation, to autonomous vehicle trajectory prediction. However, existing approaches focus on improvements on the most common scenarios without addressing the performance on rare and difficult cases. In this work, we identify a long tail behavior in the performance of state-of-the-art deep learning methods on probabilistic forecasting. We present two moment-based tailedness measurement concepts to improve performance on the difficult tail examples: Pareto Loss and Kurtosis Loss. Kurtosis loss is a symmetric measurement as the fourth moment about the mean of the loss distribution. Pareto loss is asymmetric measuring right tailedness, modeling the loss using a generalized Pareto distribution (GPD). We demonstrate the performance of our approach on several real-world datasets including time series and spatiotemporal trajectories, achieving significant improvements on the tail examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge