Tails of Triangular Flows

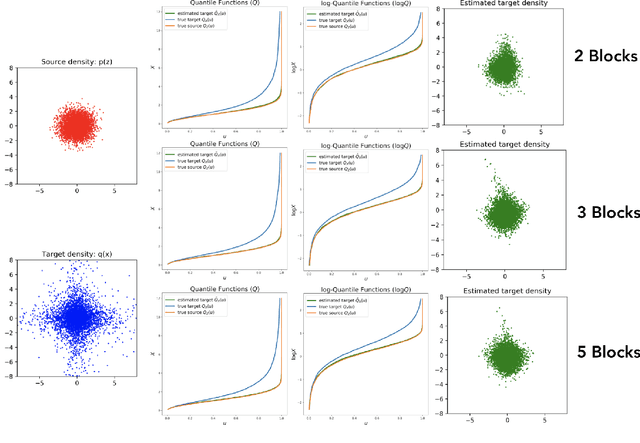
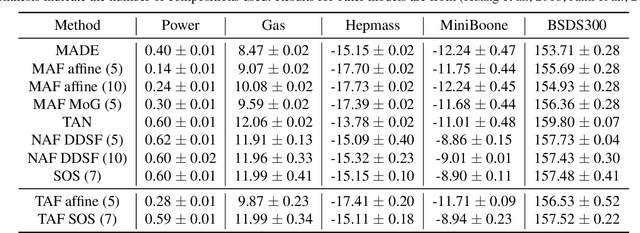
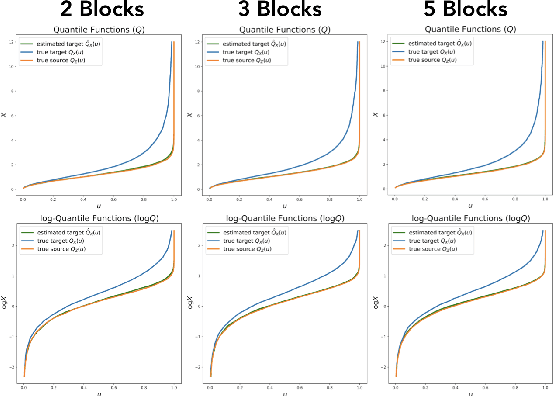
Triangular maps are a construct in probability theory that allows the transformation of any source density to any target density. We consider flow based models that learn these triangular transformations which we call triangular flows and study the properties of these triangular flows with the goal of capturing heavy tailed target distributions.In one dimension, we prove that the density quantile functions of the source and target density can characterize properties of the increasing push-forward transformation and show that no Lipschitz continuous increasing map can transform a light-tailed source to a heavy-tailed target density. We further precisely relate the asymptotic behavior of these density quantile functions with the existence of certain function moments of distributions. These results allow us to give a precise asymptotic rate at which an increasing transformation must grow to capture the tail properties of a target given the source distribution. In the multivariate case, we show that any increasing triangular map transforming a light-tailed source density to a heavy-tailed target density must have all eigenvalues of the Jacobian to be unbounded. Our analysis suggests the importance of source distribution in capturing heavy-tailed distributions and we discuss the implications for flow based models.