System Norm Regularization Methods for Koopman Operator Approximation
Paper and Code
Oct 18, 2021

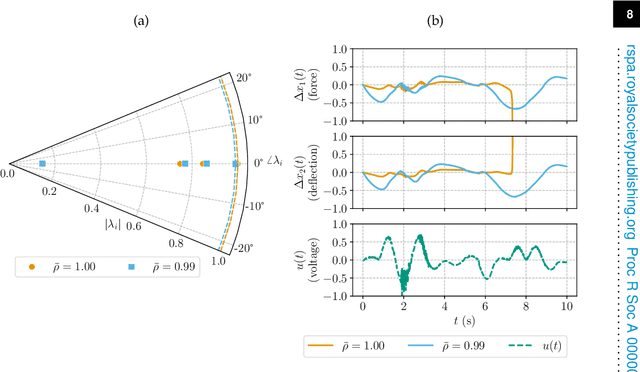
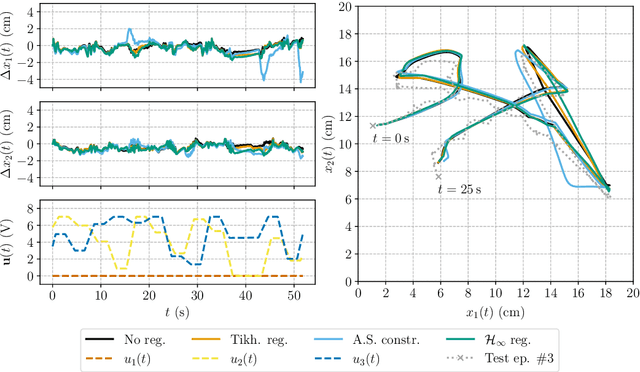
Approximating the Koopman operator from data is numerically challenging when many lifting functions are considered. Even low-dimensional systems can yield unstable or ill-conditioned results in a high-dimensional lifted space. In this paper, Extended DMD and DMD with control, two popular methods for approximating the Koopman operator, are reformulated as convex optimization problems with linear matrix inequality constraints. Both hard asymptotic stability constraints and system norm regularizers are considered as methods to improve the numerical conditioning of the approximate Koopman operator. In particular, the $\mathcal{H}_\infty$ norm is used as a regularizer to penalize the input-output gain of the linear system defined by the Koopman operator. Weighting functions are then applied to penalize the system gain at particular frequencies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge