Synergistic Scheduling of Learning and Allocation of Tasks in Human-Robot Teams

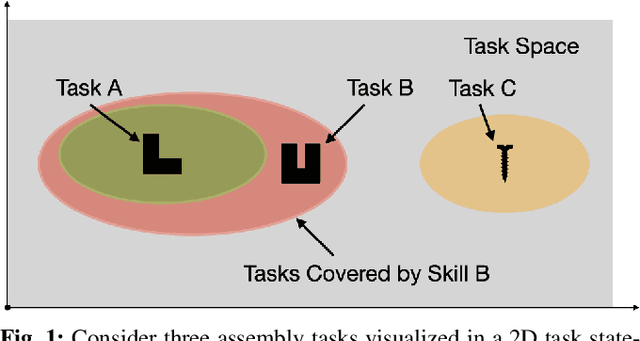
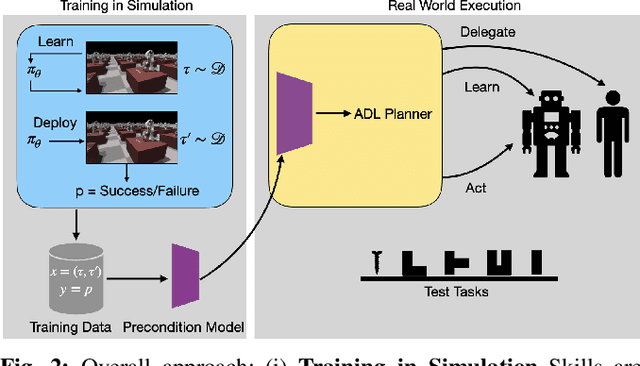
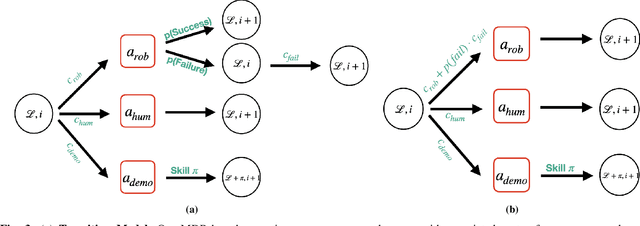
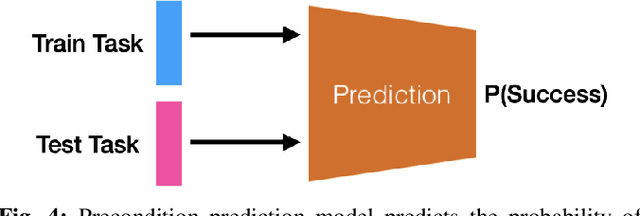
We consider the problem of completing a set of $n$ tasks with a human-robot team using minimum effort. In many domains, teaching a robot to be fully autonomous can be counterproductive if there are finitely many tasks to be done. Rather, the optimal strategy is to weigh the cost of teaching a robot and its benefit -- how many new tasks it allows the robot to solve autonomously. We formulate this as a planning problem where the goal is to decide what tasks the robot should do autonomously (act), what tasks should be delegated to a human (delegate) and what tasks the robot should be taught (learn) so as to complete all the given tasks with minimum effort. This planning problem results in a search tree that grows exponentially with $n$ -- making standard graph search algorithms intractable. We address this by converting the problem into a mixed integer program that can be solved efficiently using off-the-shelf solvers with bounds on solution quality. To predict the benefit of learning, we use an approximate simulation model of the tasks to train a precondition model that is parameterized by the training task. Finally, we evaluate our approach on peg insertion and Lego stacking tasks -- both in simulation and real-world, showing substantial savings in human effort.