Symplectic Wigner Distribution in the Linear Canonical Transform Domain: Theory and Application

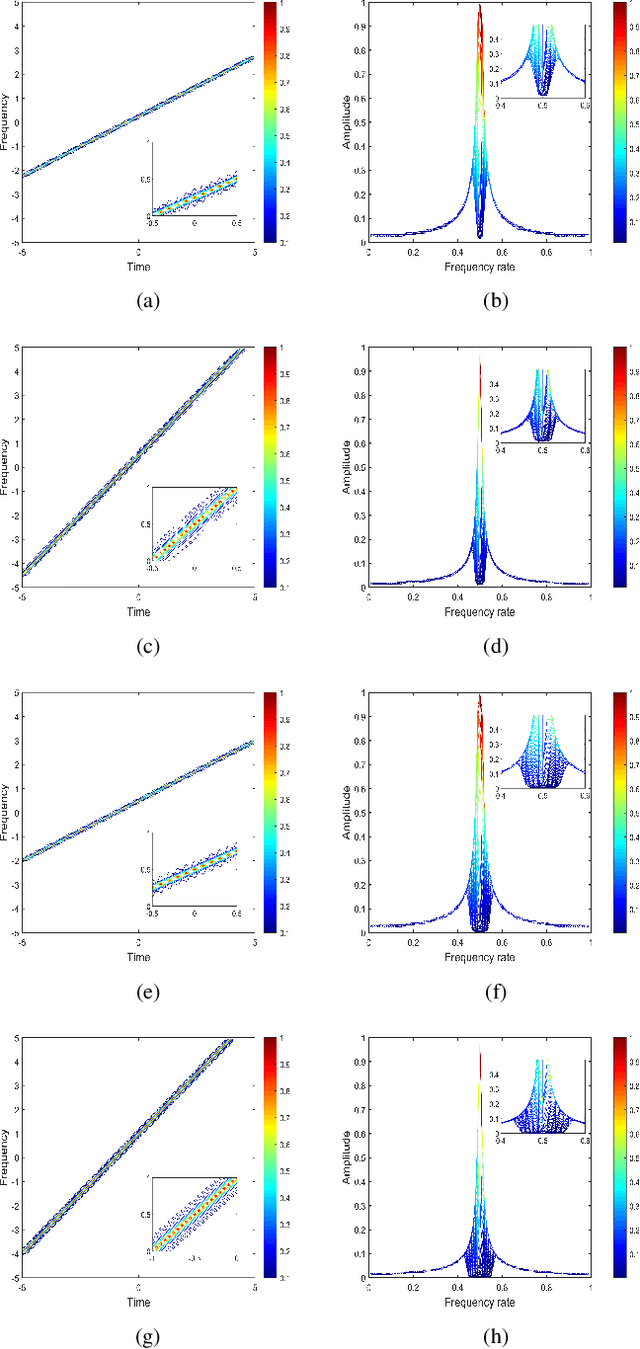
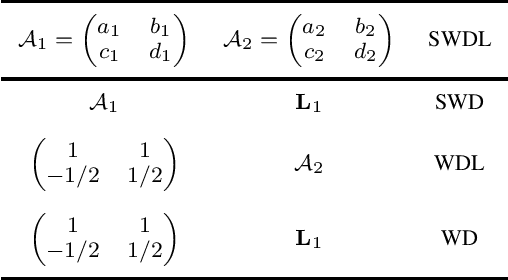
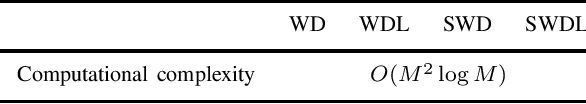
This paper devotes to combine the chirp basis function transformation and symplectic coordinates transformation to yield a novel Wigner distribution (WD) associated with the linear canonical transform (LCT), named as the symplectic WD in the LCT domain (SWDL). It incorporates the merits of the symplectic WD (SWD) and the WD in the LCT domain (WDL), achieving stronger capability in the linear frequency-modulated (LFM) signal frequency rate feature extraction while maintaining the same level of computational complexity. Some essential properties of the SWDL are derived, including marginal distributions, energy conservations, unique reconstruction, Moyal formula, complex conjugate symmetry, time reversal symmetry, scaling property, time translation property, frequency modulation property, and time translation and frequency modulation property. Heisenberg's uncertainty principles of the SWDL are formulated, giving rise to three kinds of lower bounds attainable respectively by Gaussian enveloped complex exponential signal, Gaussian signal and Gaussian enveloped chirp signal. The optimal symplectic matrices corresponding to the highest time-frequency resolution are generated by solving the lower bound optimization (minimization) problem. The time-frequency resolution of the SWDL is compared with those of the SWD and WDL to demonstrate its superiority in LFM signals time-frequency energy concentration. A synthesis example is also carried out to verify the feasibility and reliability of the theoretical analysis.