SwarmCCO: Probabilistic Reactive Collision Avoidance for Quadrotor Swarms under Uncertainty

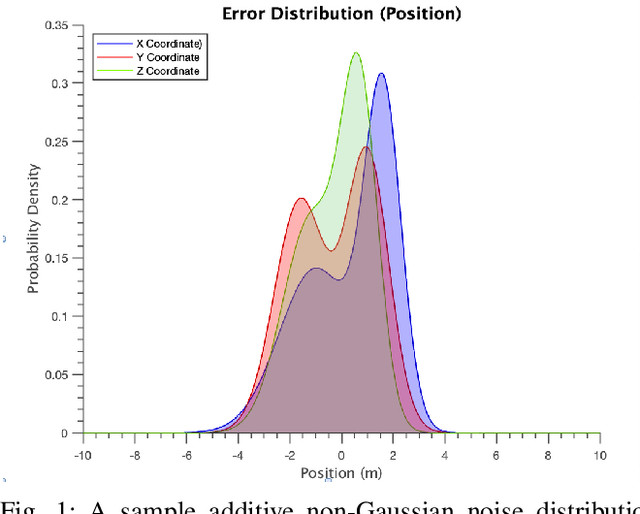
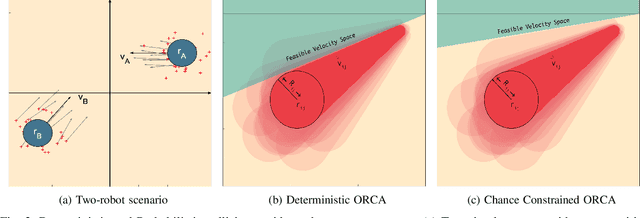
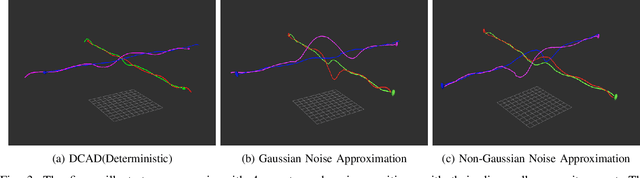
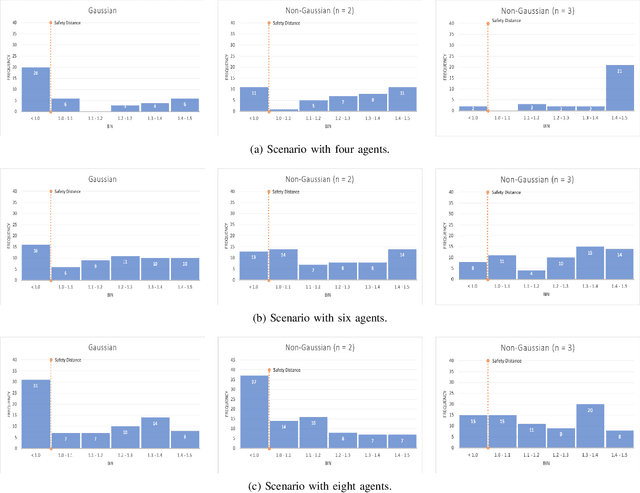
We present decentralized collision avoidance algorithms for quadrotor swarms operating under uncertain state estimation. Our approach exploits the differential flatness property and feedforward linearization to approximate the quadrotor dynamics and reciprocal collision avoidance. We account for the uncertainty in position and velocity by formulating the collision constraints as chance constraints, which describe a set of velocities that avoid collisions with a specified confidence level. We present two different methods for formulating and solving the chance constraint: our first method assumes a Gaussian noise distribution. Our second method is its extension to the non-Gaussian case by using a Gaussian Mixture Model (GMM). We reformulate the linear chance constraints into equivalent deterministic constraints on mean and covariance. Subsequently, the deterministic constraints are introduced in the MPC framework to compute a local collision-free trajectory for each quadrotor. We evaluate the proposed algorithm in simulations on benchmark scenarios and highlight its benefits over prior methods. We observe that both the Gaussian and non-Gaussian methods provide improved collision avoidance performance over the deterministic method. Further, the non-Gaussian method results in a relatively shorter path length compared to Gaussian formulations. On average, the Gaussian method requires ~5ms ms to compute a local collision-free trajectory, while our non-Gaussian method is computationally more expensive and requires ~7ms ms on average in the presence of 4 agents.