Support Feature Machines
Paper and Code
Jan 28, 2019


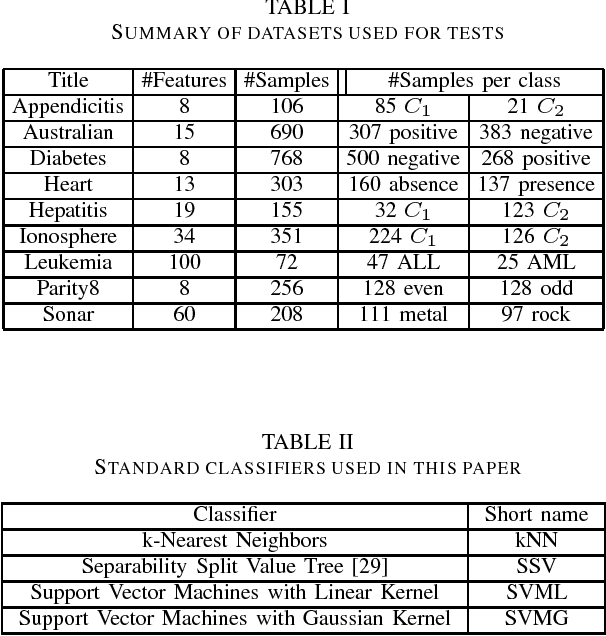
Support Vector Machines (SVMs) with various kernels have played dominant role in machine learning for many years, finding numerous applications. Although they have many attractive features interpretation of their solutions is quite difficult, the use of a single kernel type may not be appropriate in all areas of the input space, convergence problems for some kernels are not uncommon, the standard quadratic programming solution has $O(m^3)$ time and $O(m^2)$ space complexity for $m$ training patterns. Kernel methods work because they implicitly provide new, useful features. Such features, derived from various kernels and other vector transformations, may be used directly in any machine learning algorithm, facilitating multiresolution, heterogeneous models of data. Therefore Support Feature Machines (SFM) based on linear models in the extended feature spaces, enabling control over selection of support features, give at least as good results as any kernel-based SVMs, removing all problems related to interpretation, scaling and convergence. This is demonstrated for a number of benchmark datasets analyzed with linear discrimination, SVM, decision trees and nearest neighbor methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge