Supervisor Synthesis of POMDP based on Automata Learning
Paper and Code
Mar 24, 2017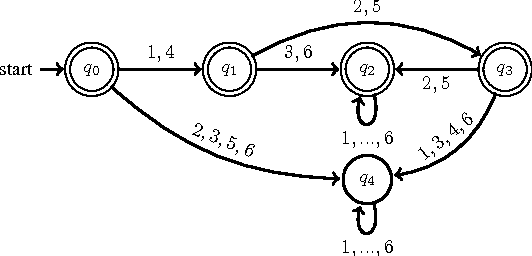
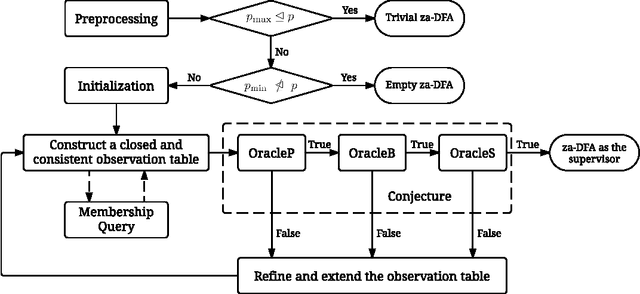
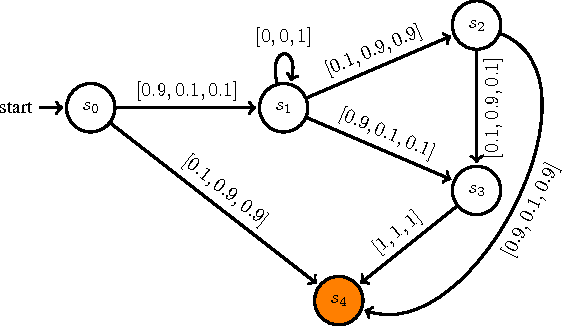
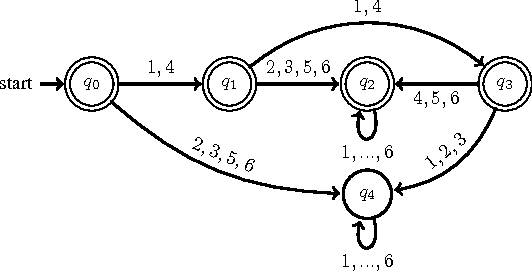
As a general and thus popular model for autonomous systems, partially observable Markov decision process (POMDP) can capture uncertainties from different sources like sensing noises, actuation errors, and uncertain environments. However, its comprehensiveness makes the planning and control in POMDP difficult. Traditional POMDP planning problems target to find the optimal policy to maximize the expectation of accumulated rewards. But for safety critical applications, guarantees of system performance described by formal specifications are desired, which motivates us to consider formal methods to synthesize supervisor for POMDP. With system specifications given by Probabilistic Computation Tree Logic (PCTL), we propose a supervisory control framework with a type of deterministic finite automata (DFA), za-DFA, as the controller form. While the existing work mainly relies on optimization techniques to learn fixed-size finite state controllers (FSCs), we develop an $L^*$ learning based algorithm to determine both space and transitions of za-DFA. Membership queries and different oracles for conjectures are defined. The learning algorithm is sound and complete. An example is given in detailed steps to illustrate the supervisor synthesis algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge