Superdirective Arrays with Finite-Length Dipoles: Modeling and New Perspectives
Paper and Code
Aug 02, 2022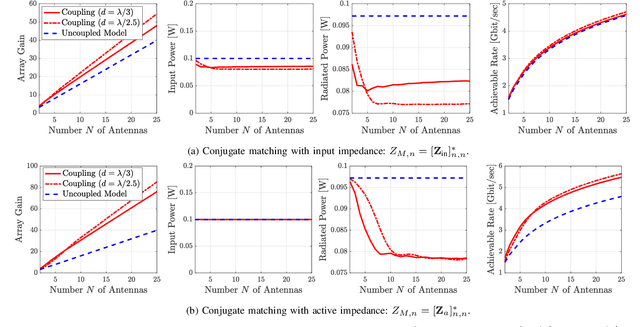
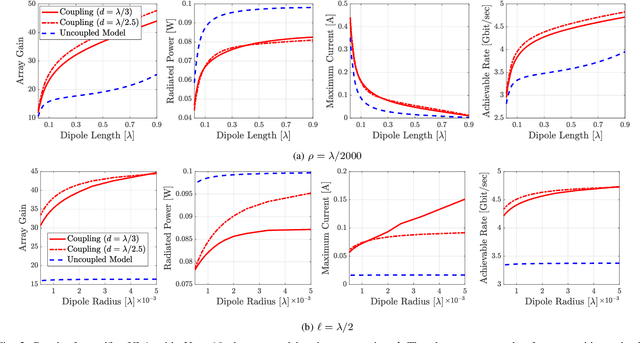
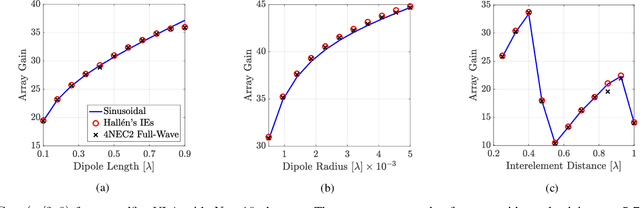
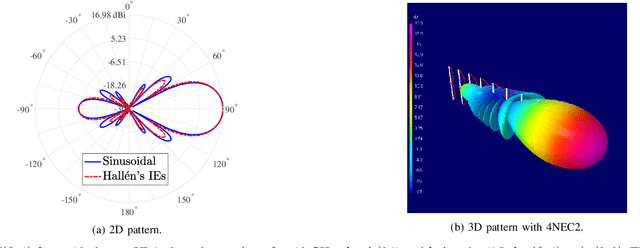
Dense arrays can facilitate the integration of multiple antennas into finite volumes. In addition to the compact size, sub-wavelength spacing enables superdirectivity for endfire operation, a phenomenon that has been mainly studied for isotropic and infinitesimal radiators. In this work, we focus on linear dipoles of arbitrary yet finite length. Specifically, we first introduce an array model that accounts for the sinusoidal current distribution (SCD) on very thin dipoles. Based on the SCD, the loss resistance of each dipole antenna is precisely determined. Capitalizing on the derived model, we next investigate the maximum achievable rate under a fixed power constraint. The optimal design entails conjugate power matching along with maximizing the array gain. Our theoretical analysis is corroborated by the method of moments under the thin-wire approximation, as well as by full-wave simulations. Numerical results showcase that a super-gain is attainable with high radiation efficiency when the dipole antennas are not too short and thin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge