Subspace Modeling for Fast Out-Of-Distribution and Anomaly Detection
Paper and Code
Mar 20, 2022

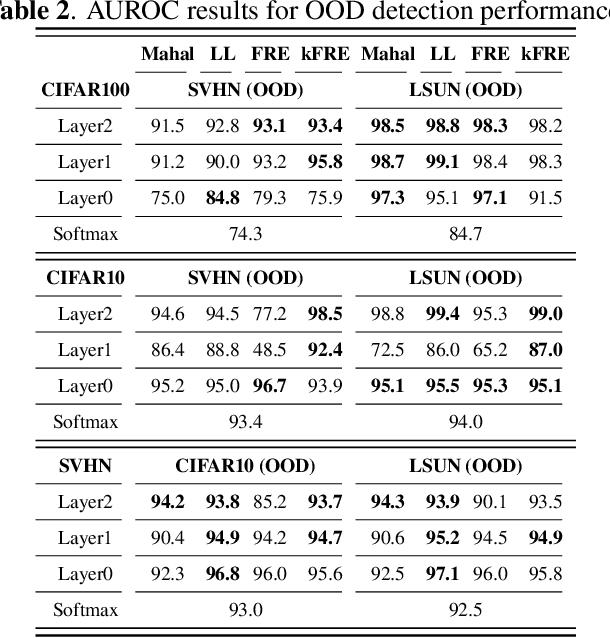
This paper presents a fast, principled approach for detecting anomalous and out-of-distribution (OOD) samples in deep neural networks (DNN). We propose the application of linear statistical dimensionality reduction techniques on the semantic features produced by a DNN, in order to capture the low-dimensional subspace truly spanned by said features. We show that the "feature reconstruction error" (FRE), which is the $\ell_2$-norm of the difference between the original feature in the high-dimensional space and the pre-image of its low-dimensional reduced embedding, is highly effective for OOD and anomaly detection. To generalize to intermediate features produced at any given layer, we extend the methodology by applying nonlinear kernel-based methods. Experiments using standard image datasets and DNN architectures demonstrate that our method meets or exceeds best-in-class quality performance, but at a fraction of the computational and memory cost required by the state of the art. It can be trained and run very efficiently, even on a traditional CPU.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge