Subregular Complexity and Deep Learning
Paper and Code
Oct 14, 2017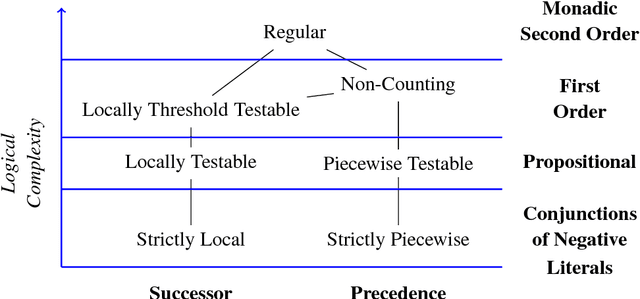

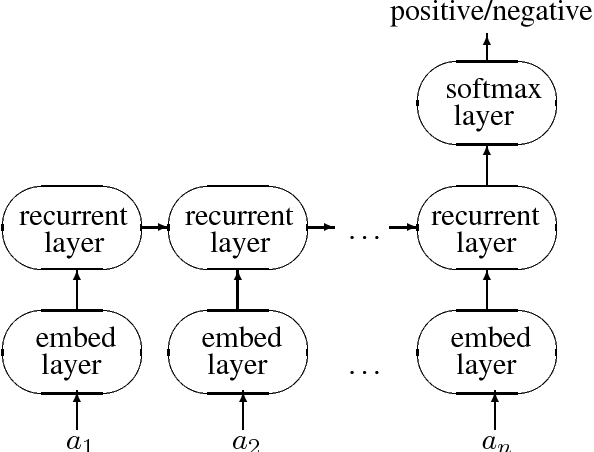
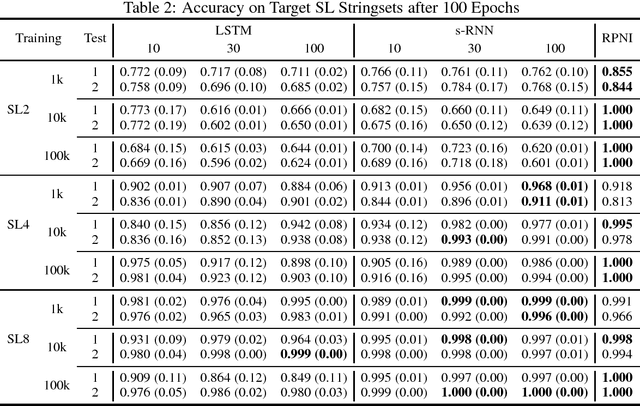
This paper argues that the judicial use of formal language theory and grammatical inference are invaluable tools in understanding how deep neural networks can and cannot represent and learn long-term dependencies in temporal sequences. Learning experiments were conducted with two types of Recurrent Neural Networks (RNNs) on six formal languages drawn from the Strictly Local (SL) and Strictly Piecewise (SP) classes. The networks were Simple RNNs (s-RNNs) and Long Short-Term Memory RNNs (LSTMs) of varying sizes. The SL and SP classes are among the simplest in a mathematically well-understood hierarchy of subregular classes. They encode local and long-term dependencies, respectively. The grammatical inference algorithm Regular Positive and Negative Inference (RPNI) provided a baseline. According to earlier research, the LSTM architecture should be capable of learning long-term dependencies and should outperform s-RNNs. The results of these experiments challenge this narrative. First, the LSTMs' performance was generally worse in the SP experiments than in the SL ones. Second, the s-RNNs out-performed the LSTMs on the most complex SP experiment and performed comparably to them on the others.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge