Structure Learning from Time Series with False Discovery Control
Paper and Code
May 24, 2018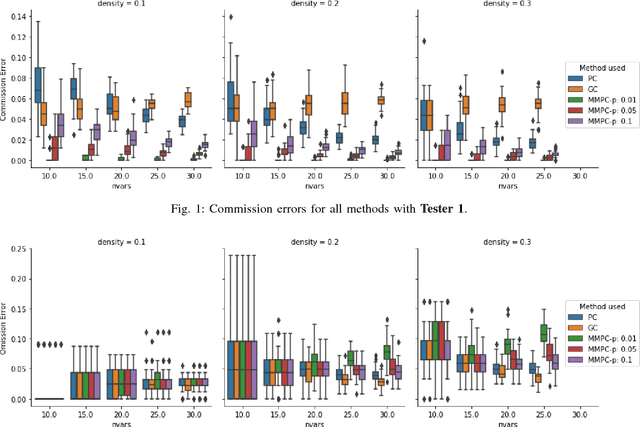
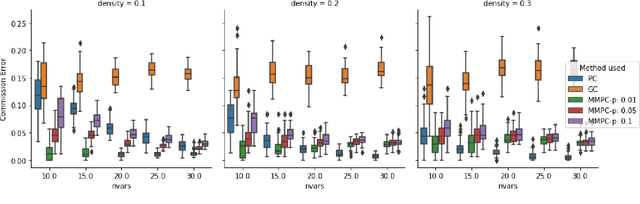
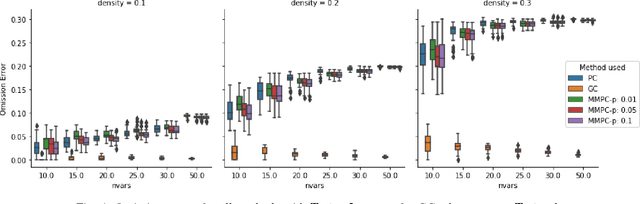
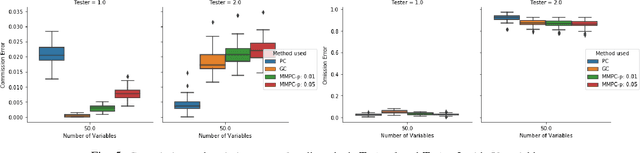
We consider the Granger causal structure learning problem from time series data. Granger causal algorithms predict a 'Granger causal effect' between two variables by testing if prediction error of one decreases significantly in the absence of the other variable among the predictor covariates. Almost all existing Granger causal algorithms condition on a large number of variables (all but two variables) to test for effects between a pair of variables. We propose a new structure learning algorithm called MMPC-p inspired by the well known MMHC algorithm for non-time series data. We show that under some assumptions, the algorithm provides false discovery rate control. The algorithm is sound and complete when given access to perfect directed information testing oracles. We also outline a novel tester for the linear Gaussian case. We show through our extensive experiments that the MMPC-p algorithm scales to larger problems and has improved statistical power compared to existing state of the art for large sparse graphs. We also apply our algorithm on a global development dataset and validate our findings with subject matter experts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge