Structural and Semantic Contrastive Learning for Self-supervised Node Representation Learning
Paper and Code
Feb 17, 2022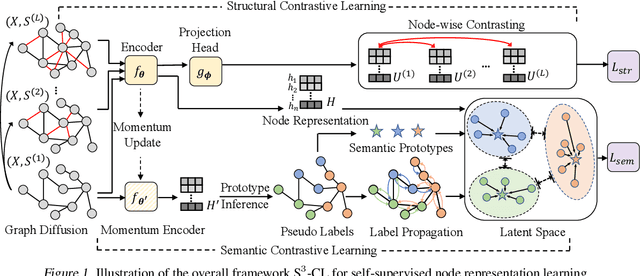
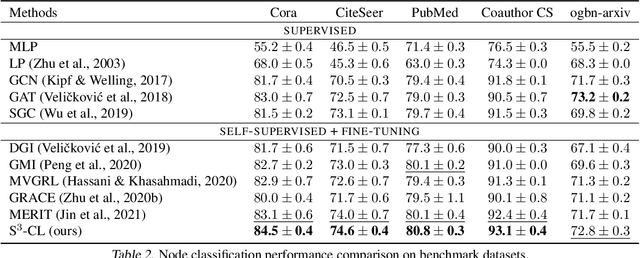
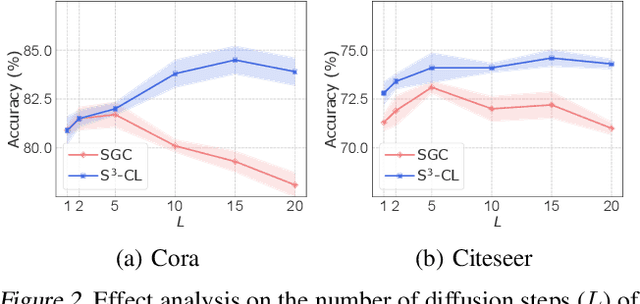
Graph Contrastive Learning (GCL) recently has drawn much research interest for learning generalizable, transferable, and robust node representations in a self-supervised fashion. In general, the contrastive learning process in GCL is performed on top of the representations learned by a graph neural network (GNN) backbone, which transforms and propagates the node contextual information based on its local neighborhoods. However, existing GCL efforts have severe limitations in terms of both encoding architecture, augmentation, and contrastive objective, making them commonly inefficient and ineffective to use in different datasets. In this work, we go beyond the existing unsupervised GCL counterparts and address their limitations by proposing a simple yet effective framework S$^3$-CL. Specifically, by virtue of the proposed structural and semantic contrastive learning, even a simple neural network is able to learn expressive node representations that preserve valuable structural and semantic patterns. Our experiments demonstrate that the node representations learned by S$^3$-CL achieve superior performance on different downstream tasks compared to the state-of-the-art GCL methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge