StreamNet: A WAE for White Matter Streamline Analysis
Paper and Code
Sep 03, 2022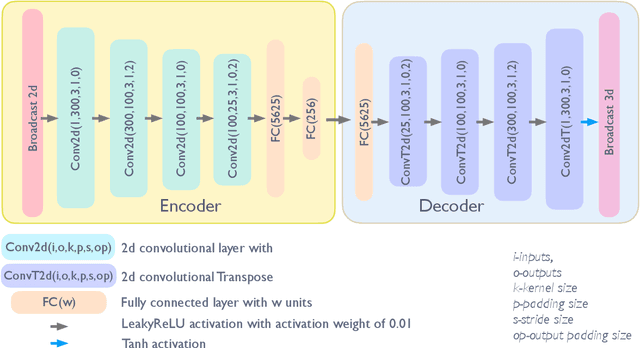

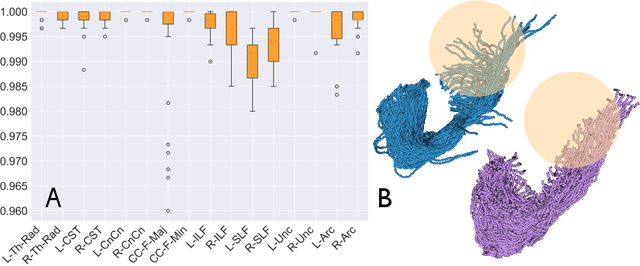
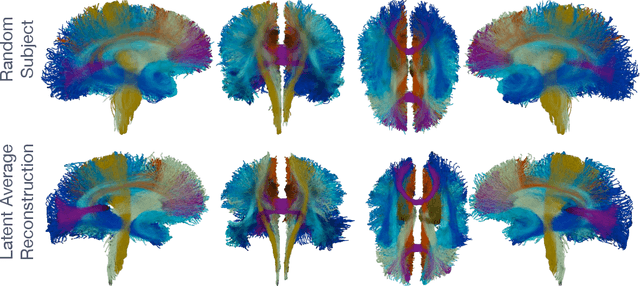
We present StreamNet, an autoencoder architecture for the analysis of the highly heterogeneous geometry of large collections of white matter streamlines. This proposed framework takes advantage of geometry-preserving properties of the Wasserstein-1 metric in order to achieve direct encoding and reconstruction of entire bundles of streamlines. We show that the model not only accurately captures the distributive structures of streamlines in the population, but is also able to achieve superior reconstruction performance between real and synthetic streamlines. Experimental model performance is evaluated on white matter streamlines resulting from T1-weighted diffusion imaging of 40 healthy controls using recent state of the art bundle comparison metric that measures fiber-shape similarities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge