Streaming Quantiles Algorithms with Small Space and Update Time
Paper and Code
Jun 29, 2019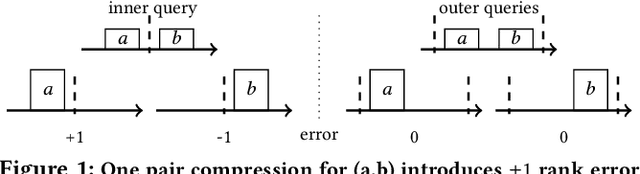
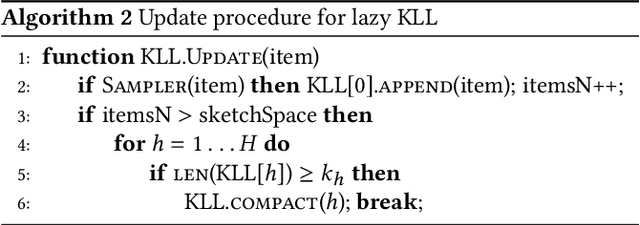

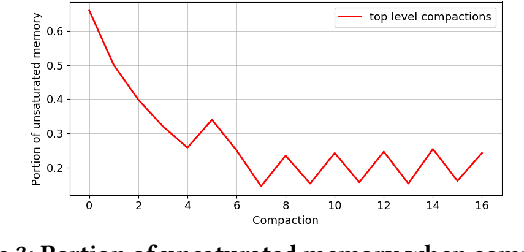
Approximating quantiles and distributions over streaming data has been studied for roughly two decades now. Recently, Karnin, Lang, and Liberty proposed the first asymptotically optimal algorithm for doing so. This manuscript complements their theoretical result by providing a practical variants of their algorithm with improved constants. For a given sketch size, our techniques provably reduce the upper bound on the sketch error by a factor of two. These improvements are verified experimentally. Our modified quantile sketch improves the latency as well by reducing the worst case update time from $O(1/\varepsilon)$ down to $O(\log (1/\varepsilon))$. We also suggest two algorithms for weighted item streams which offer improved asymptotic update times compared to na\"ive extensions. Finally, we provide a specialized data structure for these sketches which reduces both their memory footprints and update times.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge