Stochastic Submodular Maximization: The Case of Coverage Functions
Paper and Code
Nov 05, 2017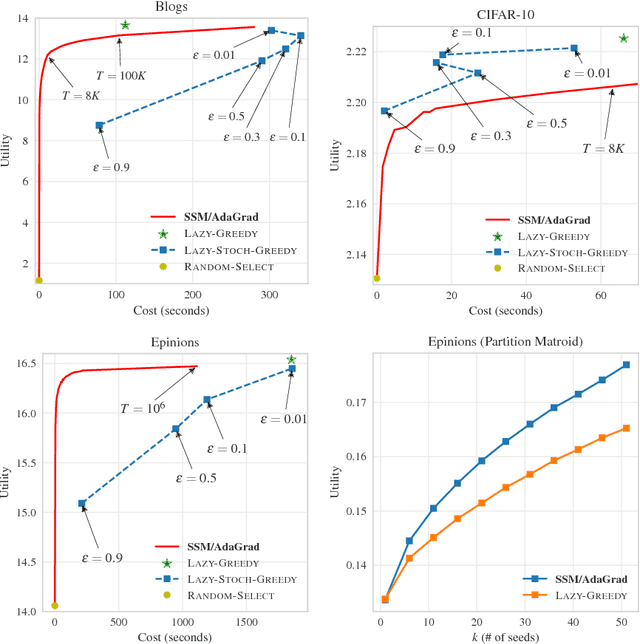
Stochastic optimization of continuous objectives is at the heart of modern machine learning. However, many important problems are of discrete nature and often involve submodular objectives. We seek to unleash the power of stochastic continuous optimization, namely stochastic gradient descent and its variants, to such discrete problems. We first introduce the problem of stochastic submodular optimization, where one needs to optimize a submodular objective which is given as an expectation. Our model captures situations where the discrete objective arises as an empirical risk (e.g., in the case of exemplar-based clustering), or is given as an explicit stochastic model (e.g., in the case of influence maximization in social networks). By exploiting that common extensions act linearly on the class of submodular functions, we employ projected stochastic gradient ascent and its variants in the continuous domain, and perform rounding to obtain discrete solutions. We focus on the rich and widely used family of weighted coverage functions. We show that our approach yields solutions that are guaranteed to match the optimal approximation guarantees, while reducing the computational cost by several orders of magnitude, as we demonstrate empirically.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge