Stochastic Recursive Momentum for Policy Gradient Methods
Paper and Code
Mar 09, 2020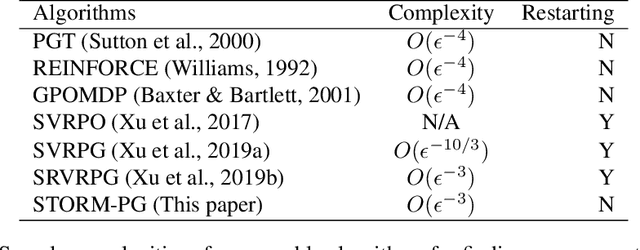


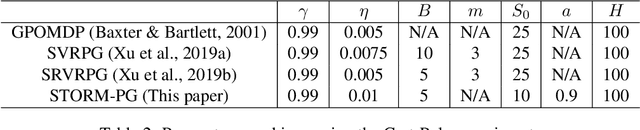
In this paper, we propose a novel algorithm named STOchastic Recursive Momentum for Policy Gradient (STORM-PG), which operates a SARAH-type stochastic recursive variance-reduced policy gradient in an exponential moving average fashion. STORM-PG enjoys a provably sharp $O(1/\epsilon^3)$ sample complexity bound for STORM-PG, matching the best-known convergence rate for policy gradient algorithm. In the mean time, STORM-PG avoids the alternations between large batches and small batches which persists in comparable variance-reduced policy gradient methods, allowing considerably simpler parameter tuning. Numerical experiments depicts the superiority of our algorithm over comparative policy gradient algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge