Stochastic Neighbor Embedding under f-divergences
Paper and Code
Nov 03, 2018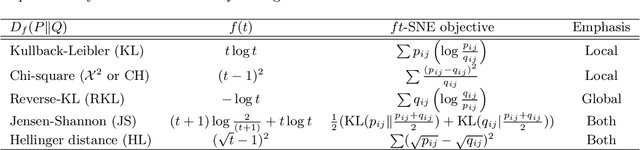
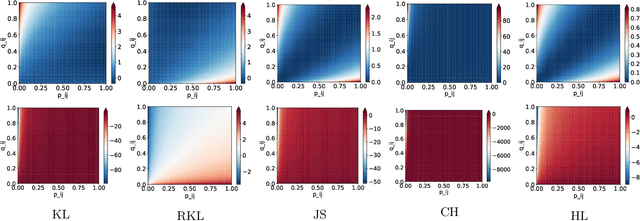
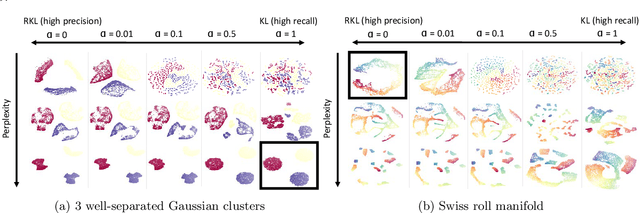
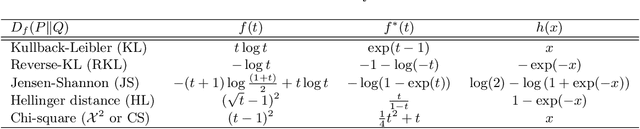
The t-distributed Stochastic Neighbor Embedding (t-SNE) is a powerful and popular method for visualizing high-dimensional data. It minimizes the Kullback-Leibler (KL) divergence between the original and embedded data distributions. In this work, we propose extending this method to other f-divergences. We analytically and empirically evaluate the types of latent structure-manifold, cluster, and hierarchical-that are well-captured using both the original KL-divergence as well as the proposed f-divergence generalization, and find that different divergences perform better for different types of structure. A common concern with $t$-SNE criterion is that it is optimized using gradient descent, and can become stuck in poor local minima. We propose optimizing the f-divergence based loss criteria by minimizing a variational bound. This typically performs better than optimizing the primal form, and our experiments show that it can improve upon the embedding results obtained from the original $t$-SNE criterion as well.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge