Stochastic modified equations and adaptive stochastic gradient algorithms
Paper and Code
Jun 20, 2017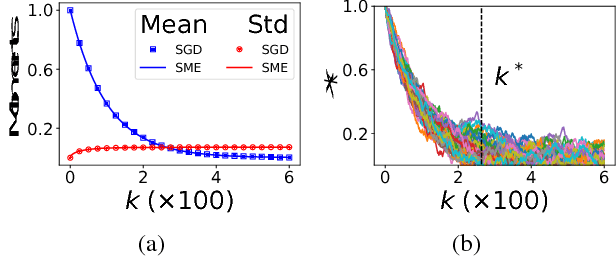
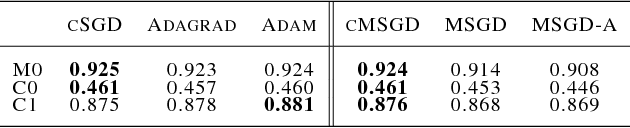
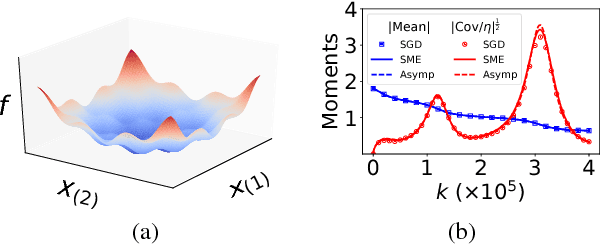
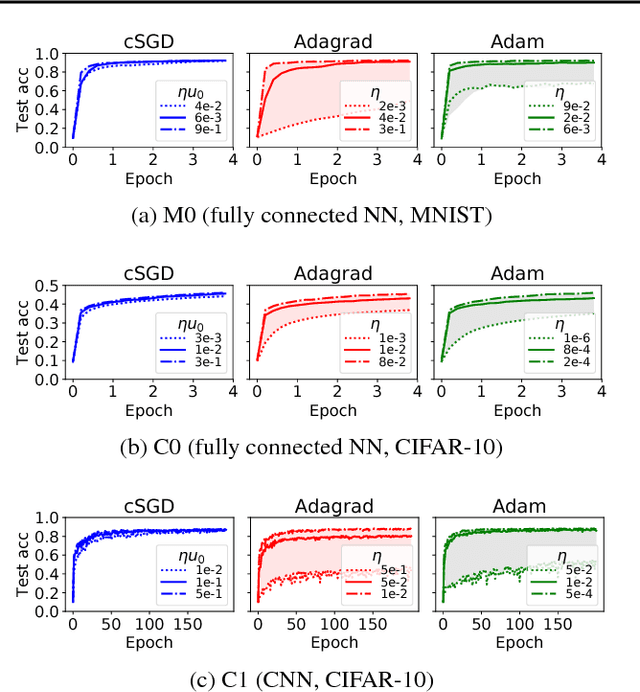
We develop the method of stochastic modified equations (SME), in which stochastic gradient algorithms are approximated in the weak sense by continuous-time stochastic differential equations. We exploit the continuous formulation together with optimal control theory to derive novel adaptive hyper-parameter adjustment policies. Our algorithms have competitive performance with the added benefit of being robust to varying models and datasets. This provides a general methodology for the analysis and design of stochastic gradient algorithms.
* Major changes including a proof of the weak approximation, asymptotic
expansions and application-oriented adaptive algorithms
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge