Stochastic Mirror Descent: Convergence Analysis and Adaptive Variants via the Mirror Stochastic Polyak Stepsize

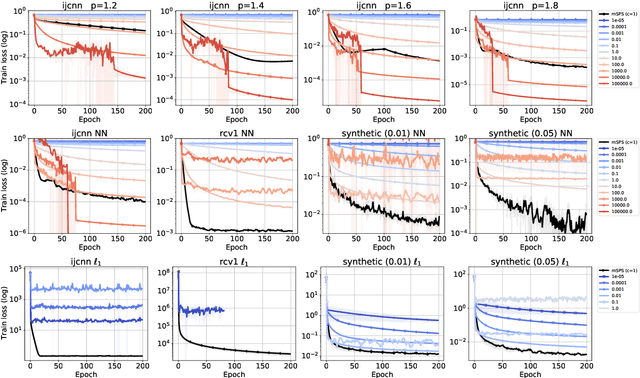
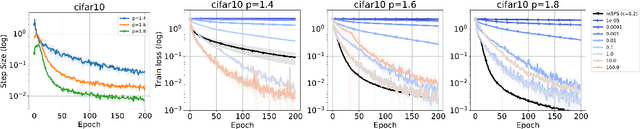
We investigate the convergence of stochastic mirror descent (SMD) in relatively smooth and smooth convex optimization. In relatively smooth convex optimization we provide new convergence guarantees for SMD with a constant stepsize. For smooth convex optimization we propose a new adaptive stepsize scheme -- the mirror stochastic Polyak stepsize (mSPS). Notably, our convergence results in both settings do not make bounded gradient assumptions or bounded variance assumptions, and we show convergence to a neighborhood that vanishes under interpolation. mSPS generalizes the recently proposed stochastic Polyak stepsize (SPS) (Loizou et al., 2021) to mirror descent and remains both practical and efficient for modern machine learning applications while inheriting the benefits of mirror descent. We complement our results with experiments across various supervised learning tasks and different instances of SMD, demonstrating the effectiveness of mSPS.