Stochastic Broadcast Control of Multi-Agent Swarms

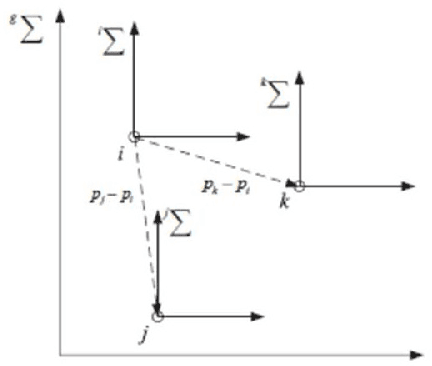
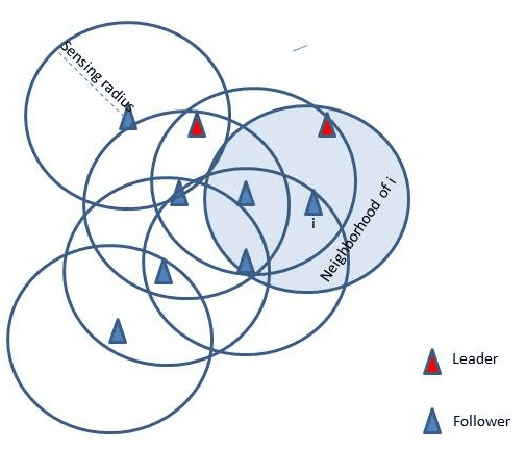
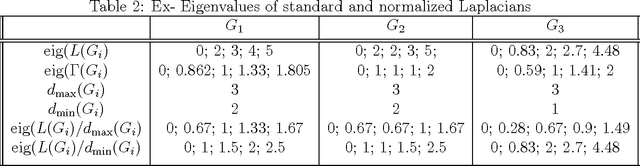
We present a model for controlling swarms of mobile agents via broadcast control, assumed to be detected by a random set of agents in the swarm. The agents that detect the control signal become ad-hoc leaders of the swarm. The agents are assumed to be velocity controlled, identical, anonymous, memory-less units with limited capabilities of sensing their neighborhood. Each agent is programmed to behave according to a linear local gathering process, based on the relative position of all its neighbors. The detected exogenous control, which is a desired velocity vector, is added by the leaders to the local gathering control. The graph induced by the agents adjacency is referred to as the visibility graph. We show that for piece-wise constant system parameters and a connected visibility graph, the swarm asymptotically aligns in each time-interval on a line in the direction of the exogenous control signal, and all the agents move with identical speed. These results hold for two models of pairwise influence in the gathering process, uniform and scaled. The impact of the influence model is mostly evident when the visibility graph is incomplete. These results are conditioned by the preservation of the connectedness of the visibility graph. In the second part of the report we analyze sufficient conditions for preserving the connectedness of the visibility graph. We show that if the visibility graph is complete then certain bounds on the control signal suffice to preserve the completeness of the graph. However, when the graph is incomplete, general conditions, independent of the leaders topology, could not be found.