Stochastic batch size for adaptive regularization in deep network optimization
Paper and Code
Apr 14, 2020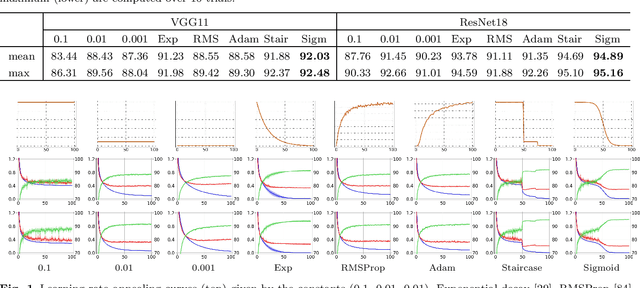

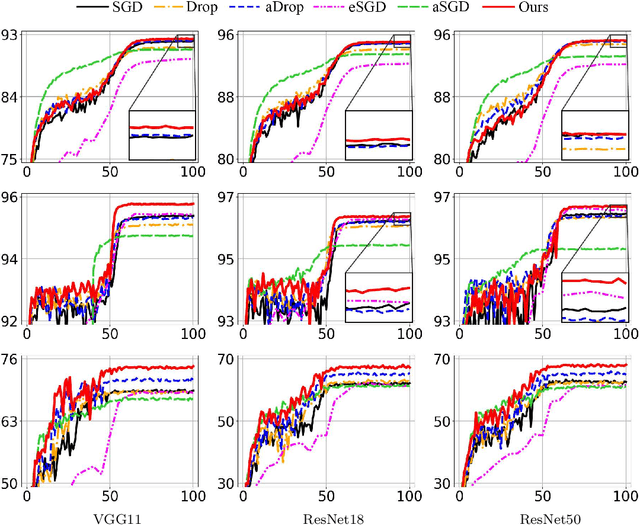

We propose a first-order stochastic optimization algorithm incorporating adaptive regularization applicable to machine learning problems in deep learning framework. The adaptive regularization is imposed by stochastic process in determining batch size for each model parameter at each optimization iteration. The stochastic batch size is determined by the update probability of each parameter following a distribution of gradient norms in consideration of their local and global properties in the neural network architecture where the range of gradient norms may vary within and across layers. We empirically demonstrate the effectiveness of our algorithm using an image classification task based on conventional network models applied to commonly used benchmark datasets. The quantitative evaluation indicates that our algorithm outperforms the state-of-the-art optimization algorithms in generalization while providing less sensitivity to the selection of batch size which often plays a critical role in optimization, thus achieving more robustness to the selection of regularity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge