Stochastic Adversarial Koopman Model for Dynamical Systems
Paper and Code
Sep 10, 2021
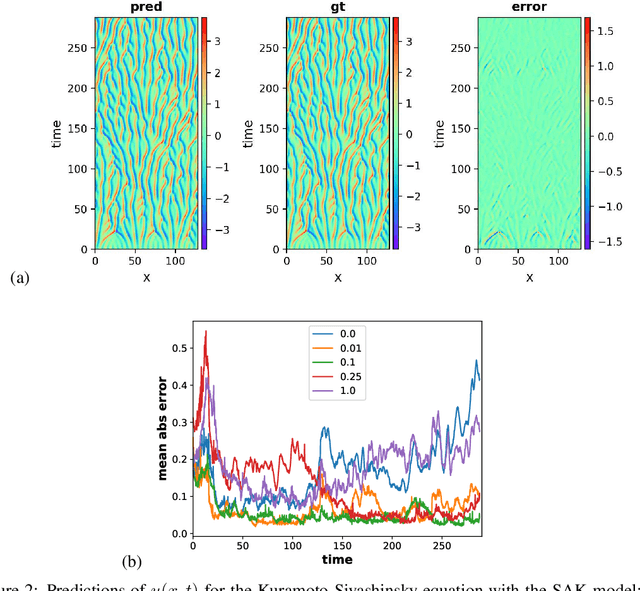
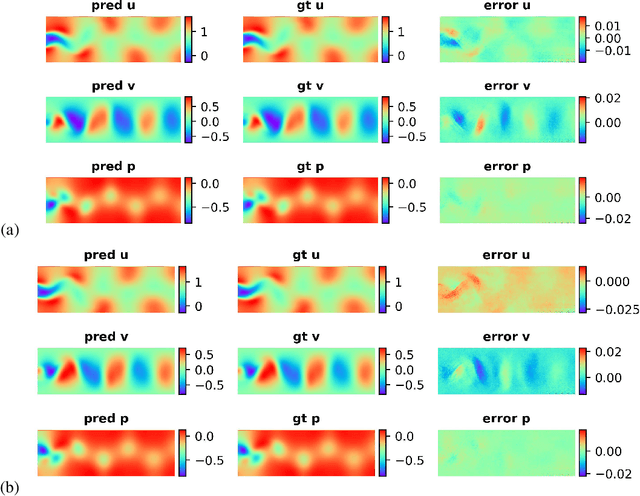
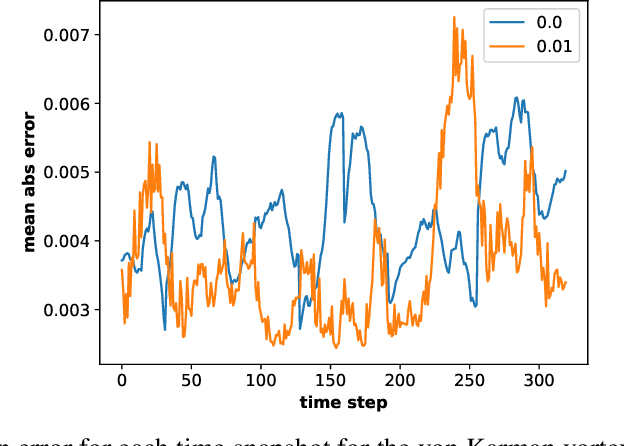
Dynamical systems are ubiquitous and are often modeled using a non-linear system of governing equations. Numerical solution procedures for many dynamical systems have existed for several decades, but can be slow due to high-dimensional state space of the dynamical system. Thus, deep learning-based reduced order models (ROMs) are of interest and one such family of algorithms along these lines are based on the Koopman theory. This paper extends a recently developed adversarial Koopman model (Balakrishnan \& Upadhyay, arXiv:2006.05547) to stochastic space, where the Koopman operator applies on the probability distribution of the latent encoding of an encoder. Specifically, the latent encoding of the system is modeled as a Gaussian, and is advanced in time by using an auxiliary neural network that outputs two Koopman matrices $K_{\mu}$ and $K_{\sigma}$. Adversarial and gradient losses are used and this is found to lower the prediction errors. A reduced Koopman formulation is also undertaken where the Koopman matrices are assumed to have a tridiagonal structure, and this yields predictions comparable to the baseline model with full Koopman matrices. The efficacy of the stochastic Koopman model is demonstrated on different test problems in chaos, fluid dynamics, combustion, and reaction-diffusion models. The proposed model is also applied in a setting where the Koopman matrices are conditioned on other input parameters for generalization and this is applied to simulate the state of a Lithium-ion battery in time. The Koopman models discussed in this study are very promising for the wide range of problems considered.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge