Statistical Characteristics of Driver Accelerating Behavior and Its Probability Model

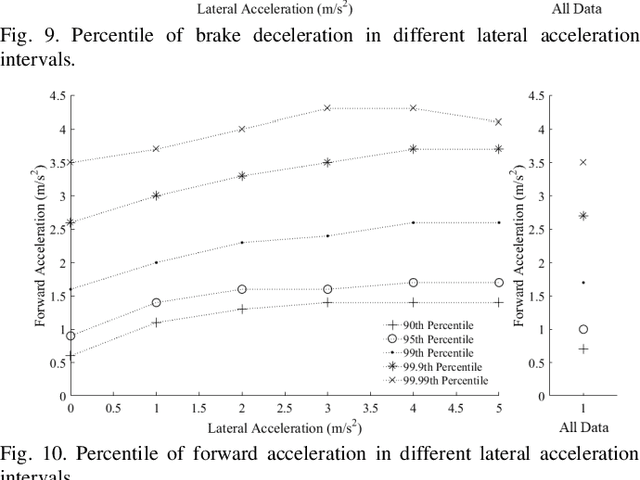
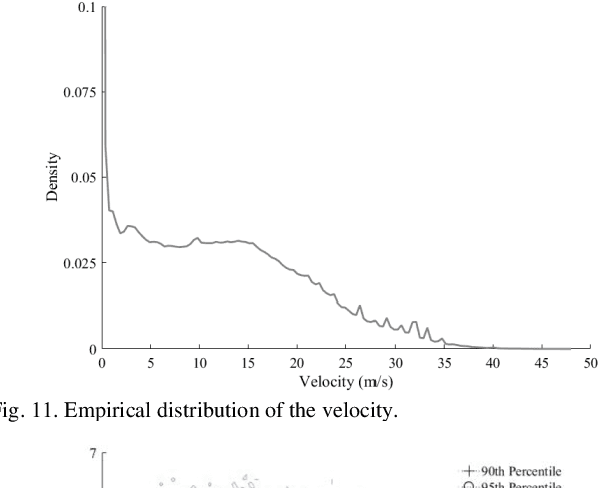
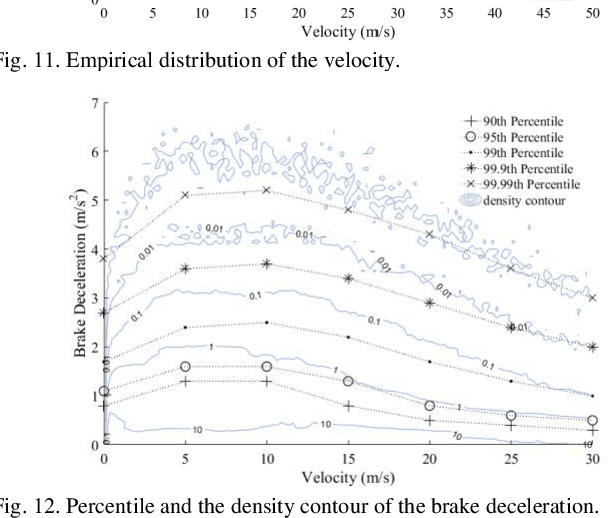
The naturalistic driving data are employed to study the accelerating behavior of the driver. Firstly, the question that whether the database is big enough to achieve a convergent accelerating behavior of the driver is studied. The kernel density estimation is applied to estimate the distributions of the accelerations. The Kullback-Liebler divergence is employed to evaluate the distinction between datasets composed of different quantity of data. The results show that a convergent accelerating behavior of the driver can be obtained by using the database in this study. Secondly, the bivariate accelerating behavior is proposed. It is shown that the bivariate distribution between longitudinal acceleration and lateral acceleration follows the dual triangle distribution pattern. Two bivariate distribution models are proposed to explain this phenomenon, i.e. the bivariate Normal distribution model (BNDM) and the bivariate Pareto distribution model (BPDM). The univariate acceleration behavior is presented to examine which model is better. It is identified that the marginal distribution and conditional distribution of the accelerations approximately follow the univariate Pareto distribution. Hence, the BPDM is a more appropriate one to describe the bivariate accelerating behavior of the driver. This reveals that the bivariate distribution pattern will never reach a circle-shaped region.